Question

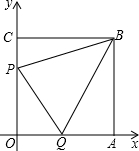如图，边长为7的正方形OABC放置在平面直角坐标系中，动点P从点C出发，以每秒1个单位的速度向O运动，点Q从点O同时出发，以每秒1个单位的速度向点A运动，到达端点即停止运动，运动时间为t秒，连PQ，BP，BQ
（1）写出B点坐标；
（2）填写下表：

时间t（单位：秒）	1	2	3	4	5	6
OP的长度
OQ的长度
PQ的长度
四边形OPBQ的面积

（1）根据你所填的数据，请你描述线段PQ的长度的变化规律并猜测PQ长度的最小值；
（2）根据你所填的数据，请问四边形OPBQ的面积是否发生变化并证明你的论断；
（3）设点M、N分别是BP、BQ的中点，写出点M，N的坐标，是否存在经过M、M两点的反比例函数？如果存在，求出t的值；如果不存在，说明理由．

Answer 1

分析：通过写点的坐标，填表，搞清楚本题的基本数量关系，每个量的变化规律，然后进行猜想；用运动时间t，表示线段OP，OQ，CP，AQ的长度，运用割补法求四边形OPBQ的面积，由中位线定理得点M（3.5，7-

t

2

），N（

t+7

2

，3.5），反比例函数图象上点的坐标特点是x_M•y_M=x_N•y_N，利用该等式求t值．

解答：解：（1）B（7，7）

（2）填写下表：

时间t（单位：秒）	1	2	3	4	5	6
OP的长度	6	5	4	3	2	1
OQ的长度	1	2	3	4	5	6
PQ的长度	37	29	5	5	29	37
四边形OPBQ的面积	24.5	24.5	24.5	24.5	24.5	24.5

①线段PQ的长度的变化规律是先减小再增大，PQ长度的最小值是

7

2

2

．
（猜到

7

2

2

得（2分），猜到5～

7

2

2

之间得1分）
②根据所填数据，四边形OPBQ的面积不会发生变化；
∵S_POQB=7×7-

7×t

2

-

7×(7-t)

2

=24.5，
∴四边形OPBQ的面积不会发生变化．

（3）点M（3.5，7-

t

2

），N（

t+7

2

，3.5），
当3.5（7-

t

2

）=

t+7

2

×3.5时，则t=3.5，
∴当t=3.5存在经过M，N两点的反比例函数．

点评：解答本题要充分利用正方形的特殊性质．注意在正方形中的特殊三角形的应用，会用运动时间表示边长，面积，搞清楚正方形中的三角形的三边关系，反比例函数图象上点的坐标特点：xy=k（定值）等，可有助于提高解题速度和准确率．