题目内容
16．某公司销售一种新型节能产品，销售价格y（元/件）与月销售量x（件）的函数关系式为y=-$\frac{1}{100}$x+120，成本为20元/件，无论销售多少，还需每月支付广告费35000元．问：当销售量x为多少时，销售的月利润最大？并求出最大利润．分析 根据等量关系“利润=销售额-成本-广告费”列出两个函数关系式，利用函数关系式求得最大值．
解答 解：设销售的月利润为w，则
W=（y-20）x-35000
=（-$\frac{1}{100}$x+120-20）x-35000
=-$\frac{1}{100}$x2+100x-35000
=-$\frac{1}{100}$（x-5000）2+215000．
答：当销售5000件时，月利润最大为215000元．
点评 本题主要考查了二次函数的应用，根据题意列出函数表达式，熟悉二次函数的性质是解决问题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
6．在一个不透明的口袋中装有大小相同的5个球，其中有3个白球，2个黑球．现每次取一个，无放回地抽取两次，则在第一次抽到白球的条件下，第二次抽到白球的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{10}$ |
7．H7N9型禽流感是一种新型的禽流感，病毒颗粒呈多元性，其中一种球形病毒的直径约为115纳米，已知1纳米=0.000 000 001米，则该种球形病毒的直径用科学记数法表示为（ ）
| A． | 1.15×10-7米 | B． | 1.15×10-8米 | C． | 1.15×10-9米 | D． | 115×10-9米 |
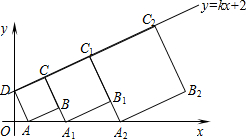在平面直角坐标系中，直线y=kx+2与y轴交于点D，点A的坐标为（1，0），以AD为边作正方形ABCD．点C在直线y=kx+2上，延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第1个正方形（即正方形ABCD）的面积为5．第2014个正方形的面积为5×$（\frac{9}{4}）^{2014}$．
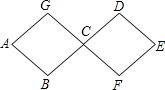如图，两个全等菱形的边长为1米，一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2014米停下，则这个微型机器人所停的点是（ ）
1．某市中考体育加试考查5个科目，具体规定是：A项目必考，再从B、C、D、E四项中随机抽考两项，则抽考两项中恰好是C、E两项的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
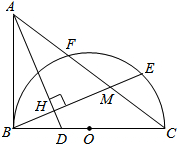如图，已知△ABC，以BC为直径，O为圆心的半圆交AC于点E，点E为弧CF的中点，连接BE交AC于点M，AD为△ABC的角平分线交BC于点D，且AD⊥BE，垂足为点H
6．下列标志中，不是中心对称的是（ ）
| A． |  | B． |  | C． |  | D． |  |