题目内容
6.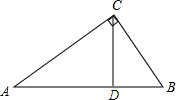 盱眙县为迎接省卫生文明城市建设,某校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
盱眙县为迎接省卫生文明城市建设,某校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
分析 根据垂线段最短可得当CD⊥AB时,CD最短,利用勾股定理计算出AB的长,再利用直角三角形的面积计算出CD长,进而可得最低造价,然后再利用勾股定理计算AD长即可.
解答 解:当CD⊥AB时,CD最短,
∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=100m,
∵S△ACB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴AC•BC=AB•CD,
80×60=100•CD,
CD=48m,
AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{6400-2304}$=64m,
故点D在距点A64m;
造价:48×100=4800(元),
答:点D在距点A64m,最低造价是4800元.
点评 此题主要考查了勾股定理的应用,以及垂线段的性质,关键是掌握直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
11.如表有六张卡片,卡片正面分别写有六个数字,背面分别写有六个字母.
将卡片正面的数由大到小排列,然后将卡片翻转,卡片上的字母组成的单词是thanks.
| 正面 | -(-1) | |-2| | (-1)3 | 0 | -3 | +5 |
| 背面 | a | h | k | n | s | t |
15.三角形的内心是( )
| A. | 三条中线的交点 | B. | 三个内角的角平分线的交点 | ||
| C. | 三条边的垂直平分线的交点 | D. | 三条高的交点 |
 如图,已知AC=AD,BC=BD,△ABC和△ABD全等吗?并说明你的理由.
如图,已知AC=AD,BC=BD,△ABC和△ABD全等吗?并说明你的理由.



 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(-2,-1)表示C点的位置,用(1,0)表示B点的位置,那么:
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(-2,-1)表示C点的位置,用(1,0)表示B点的位置,那么: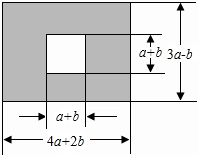 眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.