题目内容
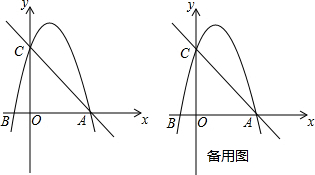
17．若二次方程x2+mx+n=0的两根分别为1与0，则抛物线y=x2+mx+n大致为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据a=1，可得出抛物线开口向上，再根据二次方程x2+mx+n=0的两根分别为1与0，即可得出答案．
解答 解：∵a=1，
∴C，D错误；
∵二次方程x2+mx+n=0的两根分别为1与0，
∴抛物线与x轴的交点坐标为（0，0），（1，0）．
故选A．
点评 本题考查了二次函数的图象，以及抛物线的开口方向、与x轴的交点坐标，是基础题，要熟练掌握．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
8．下列式子中，是分式的是（ ）
| A． | $\frac{8x}{3π}$ | B． | $\frac{{x}^{2}-{y}^{2}}{x-y}$ | C． | $\frac{x-y}{5}$ | D． | -$\frac{5}{8}$ |
5．下列式子：①5x3-2x2=3x；②2x2+3x=5x3；③4x2y-5x2y=-x2y；④5x2y-4x2y=1中，正确的有（ ）
| A． | ④ | B． | ③ | C． | ①②③ | D． | ①②③④ |
2．3的相反数是（ ）
| A． | $\frac{1}{3}$ | B． | -3 | C． | -$\frac{1}{3}$ | D． | 3 |
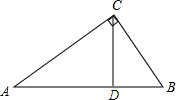盱眙县为迎接省卫生文明城市建设，某校把一块形状为直角三角形的废地开辟为植物园，如图所示，∠ACB=90°，AC=80m，BC=60m，若线段CD是一条水渠，且点D在边AB上，已知水渠的造价为100元/米，问点D在距点A多远处时，水渠的造价且点D在边AB上，已知水渠的造价为100元/米，问点D在距点A多远处时，水渠的造价最低？最低造价是多少？
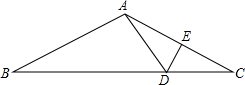如图，在△ABC中，AB=AC，AC的垂直平分线分别交BC、AC于点D、E．