题目内容
15.在一次函数y=(2a-4)•x-(1-a)中,当a为何值时:①y随x的增大而增大
②图象与y轴交点在x轴上方
③图象经过第二象限.
分析 根据一函数的图象与系数的关系列出关于a的不等式,求出a的取值范围即可.
解答 解:①∵y随x的增大而增大,
∴2a-4>0,即a>2;
②∵图象与y轴交点在x轴上方,
∴-(1-a)>0,解得a>1;
③∵图象经过第二象限,
∴$\left\{\begin{array}{l}2a-4≠0\\-(1-a)>0\end{array}\right.$,解得a>1且a≠2.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b>0时,函数的图象在一、二、三象限是解答此题的关键.

练习册系列答案
相关题目
 如图,已知AC⊥AD于A,BC⊥BD于B,且AD=BC.求证:AC=BD.
如图,已知AC⊥AD于A,BC⊥BD于B,且AD=BC.求证:AC=BD.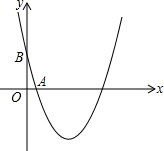 如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)
如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)