题目内容
15.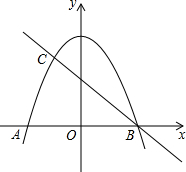 已知:如图,抛物线y=-$\frac{3}{4}$x2+3与x轴交于点A,B,与直线y=-$\frac{3}{4}$x+b交于点B,C,求直线BC所对应的函数关系式.
已知:如图,抛物线y=-$\frac{3}{4}$x2+3与x轴交于点A,B,与直线y=-$\frac{3}{4}$x+b交于点B,C,求直线BC所对应的函数关系式.
分析 根据抛物线与x轴相交,求出点A,B的坐标,根据点B在直线上,求出直线解析式.
解答 解:∵抛物线$y=-\frac{3}{4}{x}^{2}+3$与x轴相交于点A、B,
∴$-\frac{3}{4}{x}^{2}+3$=0,解得:x1=-2,x2=2,
∴点A(-2,0),点B(2,0),
∵点B(2,0)在直线y=$-\frac{3}{4}x+b$,
∴$-\frac{3}{4}×2+b=0$,解得:b=$\frac{3}{2}$,
∴直线BC的解析式为:$y=-\frac{3}{4}x+\frac{3}{2}$.
点评 本题主要考查抛物线与x轴的交点及待定系数法求解析式,求出点B的坐标是解决此题的关键.

练习册系列答案
相关题目
6.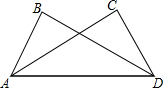 如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
 如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
20.在数$\sqrt{2}$,π,-$\frac{1}{7}$,0.3333…中,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |