题目内容
3.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明.
分析 (1)由平行四边形的判定定理容易得出结果;
(2)连接AC,由SSS证明△ABC≌CDA,得出对应角相等∠BAC=∠DCA,∠BCA=∠DAC,证出AB∥DC,BC∥AD,即可得出结论.
解答 解:(1)补全已知和求证:
已知:在四边形ABCD中,BC=AD,AB=CD.
求证:四边形ABCD是平行四边形.
故答案为:CD;平行;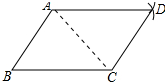
(2)证明:如图,连结AC,
在△ABC和△CDA中,
$\left\{\begin{array}{l}{AB=CD}\\{CB=DA}\\{AC=CA}\end{array}\right.$,
∴△ABC≌CDA(SSS),
∴∠BAC=∠DCA,∠BCA=∠DAC,
∴AB∥DC,BC∥AD,
∴四边形ABCD是平行四边形.
点评 本题考查了平行四边形的判定定理、全等三角形的判定方法、平行线的判定;熟练掌握平行四边形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知3x=8,3y=2,则3x+y的值是( )
| A. | 4 | B. | 6 | C. | 10 | D. | 16 |
13.下列计算中,正确的是( )
| A. | 2a3(-a2)=-2a5 | B. | (a-b)2=a2-b2 | C. | (-a)5÷(-a)2=a3 | D. | (-3)-1=3 |
20.下列计算正确的是( )
| A. | a•a2=a2 | B. | (a2)3=a5 | C. | 3a2•5a3=15a6 | D. | a5÷a2=a3 |
12.矩形具有而一般的平行四边形不一定具有的特征( )
| A. | 对角相等 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对边相等 |
 你知道古代数学家怎样解一元二次方程吗?以x2-2x-3=0为例,大致过程如下:
你知道古代数学家怎样解一元二次方程吗?以x2-2x-3=0为例,大致过程如下: 如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC. 如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.