Question

10．如图①，点O为直线AB上一点，射线OC⊥AB，垂足为O，将一直角三角板的60°角的顶点放在点O处，斜边OE在射线OB上，直角顶点D在直线AB的下方．
（1）在图①中，求∠AOD和∠COD的度数（直接写出结果）
（2）将图①中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第x秒时，OD边恰好平分∠BOC，第y秒时，OD边在∠AOC的平分线上，请分别求出x、y的值；
（3）将图①中的三角板绕点O顺时针旋转至图②，使OD边在∠AOC的内部，OE边在∠AOC的外部，请探究：∠AOE与∠DOC之间的数量关系，并说明理由．

Answer 1

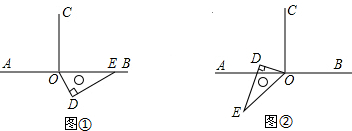
分析 （1）根据平角定义求∠AOD的度数，根据垂直定义求∠COD的度数；
（2）如图②，根据角平分线定义和旋转性质列一元一次方程求出x的值；
如图③，根据角平分线定义和旋转性质列一元一次方程求出x的值；
（3）利用∠EOC列等式，可得结论．

解答 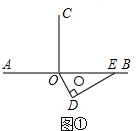解：（1）如图①，∵∠AOD+∠DOE=180°，∠DOE=60°，
∴∠AOD=180°-60°=120°，
∵OC⊥AB，
∴∠COE=90°，
∴∠COD=∠COE+∠DOE=90°+60°=150°；
则∠AOD=120°，∠COD=150°，
（2）当OD边恰好平分∠BOC时，如图②，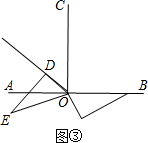
由题意得：5x=60+45，
解得：x=21秒，
当OD边在∠AOC的平分线上时，如图③，
由题意得：5y=60+90+45，
y=39秒；
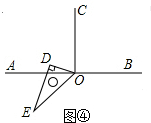
（3）如图④，由图可知：∠AOE+90°=∠DOC+60°，
∴∠AOE与∠DOC之间的数量关系是：∠DOC-∠AOE=30°．

点评 本题是角的计算问题，考查了角的和与差、角平分线、垂线的性质，明确角平分线将角平分成相等的两个角，认真观察角的大小及和与差，与三角板各角的度数相结合，同时利用旋转前后的两个角相等，列方程得出结论．