题目内容
7.已知二次函数y=$\frac{1}{2}{x^2}$+x+4(1)试确定抛物线的开口方向,顶点和对称轴;
(2)说明该抛物线怎样由抛物线y=-$\frac{1}{2}{x^2}$平移得到.
分析 (1)利用配方法得出抛物线解析式是顶点式,根据顶点式的坐标特点求开口方向,顶点坐标及对称轴;
(2)利用轴对称和平移的方法得出两个函数之间的关系.
解答 解:(1)y=$\frac{1}{2}{x^2}$+x+4=$\frac{1}{2}$(x+1)2+$\frac{7}{2}$
抛物线的开口方向向上、顶点坐标为(-1,$\frac{7}{2}$),对称轴为x=-1.
(2)将二次函数y=-$\frac{1}{2}{x^2}$作关于x的轴对称函数y=$\frac{1}{2}{x^2}$,再进一步把图象向左平移1个单位,再向上平移$\frac{7}{2}$个单位可得到y=$\frac{1}{2}{x^2}$+x+4的图象.
点评 此题考查二次函数的性质,根据抛物线的顶点式,可确定抛物线的开口方向,顶点坐标(对称轴),最大(最小)值,增减性等.

练习册系列答案
相关题目
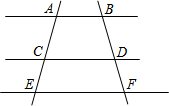 如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是$\frac{3}{7}$.
如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是$\frac{3}{7}$.