题目内容
5.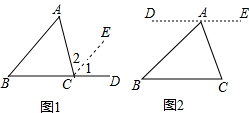 我们都知道“三角形的内角和等于180°”,如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的,请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整.
我们都知道“三角形的内角和等于180°”,如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的,请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整.已知:△ABC.
求证:∠BAC+∠B+∠C=180°.
证明:如图2,过点A作直线DE∥BC.
分析 利用平行线的性质,得到两对角相等,通过等量代换借助平角的定义可得三角形的内角和为180°.
解答  证明:过点A作直线DE∥BC,
证明:过点A作直线DE∥BC,
∵DE∥BC,
∴∠DAB=∠B,∠EAC=∠C,
∵∠DAB+∠EAC+∠BAC=180°,
∴∠B+∠C+∠BAC=180°,即三角形的内角的和等于180°.
点评 本题考查的是三角形内角和定理,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目
15.下列各数中,是无理数的是( )
| A. | $\sqrt{4}$ | B. | -2 | C. | 0 | D. | -π |
16.估算$\sqrt{5}$的大小,四舍五入到十分位是( )
| A. | 2.1 | B. | 2.2 | C. | 2.3 | D. | 2.4 |
13.与点P(5,-3)关于x轴对称的点的坐标是( )
| A. | (5,3) | B. | (-5,3) | C. | (-3,5) | D. | (3,-5) |
20.某校欲招聘一名教师,计划将面试成绩与笔试成绩按6:4计算总分并择优录取,下面是两名候选人的测试成绩,则该校应录取的是乙.(填“甲”或“乙”)
| 候选人 | 甲 | 乙 | |
| 测试成绩 (百分制) | 面试 | 86 | 92 |
| 笔试 | 90 | 83 | |