题目内容
若△ABC相似△A′B′C′,面积比为1:2,则△ABC与△A′B′C′的相似比为( )
A、1:
| ||
| B、1:4 | ||
| C、4:1 | ||
D、
|
考点:相似三角形的性质
专题:
分析:由△ABC相似△A′B′C′,面积比为1:2,根据相似三角形的面积比等于相似比的平方,即可求得答案.
解答:解:∵△ABC相似△A′B′C′,面积比为1:2,
∴△ABC与△A′B′C′的相似比为:1:
.
故选A.
∴△ABC与△A′B′C′的相似比为:1:
| 2 |
故选A.
点评:此题考查了相似三角形的性质.此题比较简单,注意熟记定理是解此题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,直线L1∥L2,则∠α为( )
如图,直线L1∥L2,则∠α为( )| A、150° | B、140° |
| C、130° | D、120° |
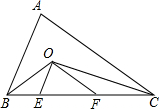 如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长.
如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长. 如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯
如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯 如图,已知:∠1=∠C,∠2+∠3=180°.由此你能得到AB与EF平行吗?请说明理由.
如图,已知:∠1=∠C,∠2+∠3=180°.由此你能得到AB与EF平行吗?请说明理由.