题目内容
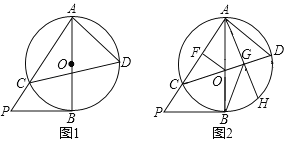
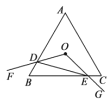
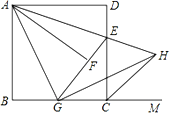
【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AB＝6cm，E是线段AB上一动点，D是BC的中点，过点C作射线CG，使CG∥AB，连接ED，并延长ED交CG于点F，连接AF．设A，E两点间的距离为xcm，A，F两点间的距离为y1cm，E，F两点间的距离为y2cm．小丽根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小丽的探究过程，请补充完整：
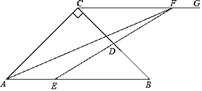
（1）按照表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
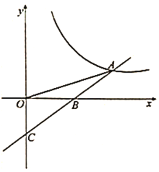
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；
（3）结合函数图象，解决问题：当△AEF为等腰三角形时，AE的长度约为 cm．
【答案】（1）4.24；（2）见解析；（3）3.50或5或6．
【解析】
（1）当x＝3时，点E是AB的中点，易证△ECF是等腰直角三角形，EF＝
EC＝3≈4.24．
（2）利用描点法画出函数图象即可解决问题．
（3）由直线y＝x与两个函数图象的交点A，B，以及函数y1与函数y2的交点C的横坐标可知，当△AEF为等腰三角形时AE的长度．
解：（1）当x＝3时，点E是AB的中点，易证△ECF是等腰直角三角形，EF＝ EC＝3≈4.24．
（2）函数图象如图所示：
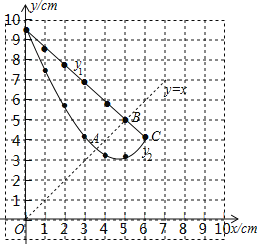
（3）由直线y＝x与两个函数图象的交点A，B，以及函数y1与函数y2的交点C的横坐标可知，当△AEF为等腰三角形时，AE的长度约为3.50或5或6．
故答案为3.50或5或6．
【题目】时代中学从学生兴趣出发，实施体育活动课走班制.为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1200名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
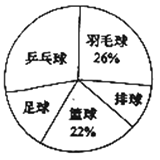
解答下列问题：
（1）这次抽样调查中的样本是________；
（2）统计表中，
________，
________；
（3）试估计上述1200名学生中最喜欢乒乓球运动的人数.
