题目内容
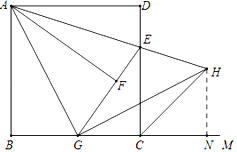
【题目】如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.
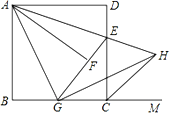
【答案】AG是∠BAF的平分线,GA是∠BGF的平分线;CH是∠DCN的平分线;GH是∠EGM的平分线;理由见解析
【解析】
过点H作HN⊥BM于N,利用正方形的性质及轴对称的性质,证明△ABG≌△AFG,可推出AG是∠BAF的平分线,GA是∠BGF的平分线;证明△ABG≌△GNH,推出HN=CN,得到∠DCH=∠NCH,推出CH是∠DCN的平分线;再证∠HGN=∠EGH,可知GH是∠EGM的平分线.
过点H作HN⊥BM于N,
则∠HNC=90°,
∵四边形ABCD为正方形,
∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°,
①∵将△ADE沿AE所在的直线折叠得到△AFE,
∴△ADE≌△AFE,
∴∠D=∠AFE=∠AFG=90°,AD=AF,∠DAE=∠FAE,
∴AF=AB,
又∵AG=AG,
∴Rt△ABG≌Rt△AFG(HL),
∴∠BAG=∠FAG,∠AGB=∠AGF,
∴AG是∠BAF的平分线,GA是∠BGF的平分线;
②由①知,∠DAE=∠FAE,∠BAG=∠FAG,
又∵∠BAD=90°,
∴∠GAF+∠EAF=![]() ×90°=45°,
×90°=45°,
即∠GAH=45°,
∵GH⊥AG,
∴∠GHA=90°﹣∠GAH=45°,
∴△AGH为等腰直角三角形,
∴AG=GH,
∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,
∴∠BAG=∠NGH,
又∵∠B=∠HNG=90°,AG=GH,
∴△ABG≌△GNH(AAS),
∴BG=NH,AB=GN,
∴BC=GN,
∵BC﹣CG=GN﹣CG,
∴BG=CN,
∴CN=HN,
∵∠DCM=90°,
∴∠NCH=∠NHC=![]() ×90°=45°,
×90°=45°,
∴∠DCH=∠DCM﹣∠NCH=45°,
∴∠DCH=∠NCH,
∴CH是∠DCN的平分线;
③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,
由①知,∠AGB=∠AGF,
∴∠HGN=∠EGH,
∴GH是∠EGM的平分线;
综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,
GH是∠EGM的平分线.

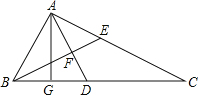
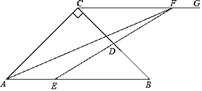
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED,并延长ED交CG于点F,连接AF.设A,E两点间的距离为xcm,A,F两点间的距离为y1cm,E,F两点间的距离为y2cm.小丽根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小丽的探究过程,请补充完整:
(1)按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:当△AEF为等腰三角形时,AE的长度约为 cm.