题目内容
8. 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是$\widehat{BF}$的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是$\widehat{BF}$的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
分析 (1)连接OC,如图,利用切线的性质得OC⊥DE,再利用圆周角定理得到∠BAC=∠EAC,加上∠BAC=∠OCA,所以∠EAC=∠OCA.则OC∥AE,从而得到AE⊥DE;
(2)连接BF交OC于G,如图,利用圆周角定理得到∴∠BFA=90°.易得四边形CEFG是矩形.则CO⊥BF,CF=GF,利用垂径定理得到BG=GF,再在Rt△ABF中利用含30度的直角三角形三边的关系得到BF=$\sqrt{3}$AF=4$\sqrt{3}$,则BG=GF=2$\sqrt{3}$,从而得到CE的长.
解答  (1)证明:连接OC,如图,
(1)证明:连接OC,如图,
∵DE切⊙O于C,
∴OC⊥DE,
∵点C是$\widehat{BF}$的中点,
∴∠BAC=∠EAC,
∵OC=OA,
∴∠BAC=∠OCA,
∴∠EAC=∠OCA.
∴OC∥AE.
∴AE⊥DE;
(2)解:连接BF交OC于G,如图,
∵AB是⊙O直径,
∴∠BFA=90°.
易得四边形CEFG是矩形.
∴CO⊥BF,CF=GF,
∴BG=GF,
在Rt△ABF中,∠BAE=60°,AF=4,
∴BF=$\sqrt{3}$AF=4$\sqrt{3}$,
∴BG=GF=2$\sqrt{3}$
∴CE=2$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.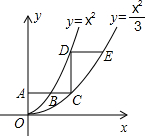 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
 如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )
如图,平行于x轴的直线AC分别交抛物线y1=x2与y2=$\frac{x^2}{3}$于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC交y2于点E,则$\frac{DE}{AB}$的值是( )| A. | 2 | B. | y=$\frac{3}{2}$ | C. | 3-$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
19.今年1~2月,我市完成固定资产投资201.4亿元,增速21%,高于全省平均增速8.6个百分点,增速继续保持全省第一,数据201.4亿用科学记数法表示为( )
| A. | 201.4×108 | B. | 2.014×108 | C. | 2.014×109 | D. | 2.014×1010 |
16.2016年12月17日,鲁南高铁临沂至曲阜段全面开工,工程正线全长约138000米,用科学记数法表示正确的是( )
| A. | 138×103米 | B. | 13.8×104米 | C. | 1.38×105米 | D. | 1.38×103米 |
13.若一个多边形的内角和为720°,则该多边形为( )边形.
| A. | 四 | B. | 五 | C. | 六 | D. | 七 |
17.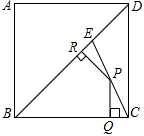 如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )
如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )
 如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )
如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
 如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).
如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).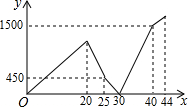 小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.
小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.