题目内容
11.已知⊙O的半径为2,则其内接正三角形的面积为3$\sqrt{3}$.分析 连接OB、OC,作OD⊥BC于D,则∠ODB=90°,BD=CD,∠OBC=30°,由含30°角的直角三角形的性质得出OD,由勾股定理求出BD,得出BC,根据△ABC的面积=3S△OBC计算即可.
解答 解:如图所示,
连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,BD=CD,∠OBC=30°,
∴OD=$\frac{1}{2}$OB=1,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{3}$,
∴BC=2BD=2$\sqrt{3}$,
∴△ABC的面积=3S△OBC=3×$\frac{1}{2}$×BC×OD=3×$\frac{1}{2}$×2$\sqrt{3}$×1=3$\sqrt{3}$.
点评 本题考查了等边三角形的性质、垂径定理、勾股定理、三角形面积的计算;熟练掌握正三角形和圆的关系,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
20.如果点A(x1,y1),B(x2,y2)都在反比例函数y=-$\frac{2}{x}$的图象上,并且x1<x2<0,那么下列各式正确的是( )
| A. | y2>y1>0 | B. | y1<y2<0 | C. | y1>y2>0 | D. | y2<y1<0 |
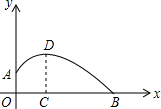 如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.
如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.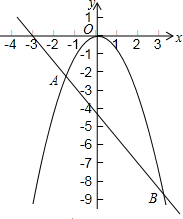 如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.
如图所示,抛物线${y_1}=-{x^2}$与直线${y_2}=-\frac{3}{2}x-\frac{9}{2}$交于A,B两点.