题目内容
4.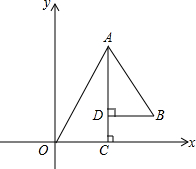 如图,Rt△AOC和Rt△ABD,∠OCA=∠AOB=90°,∠OAC=∠CAB=30°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=4,则k的值为$\sqrt{3}$.
如图,Rt△AOC和Rt△ABD,∠OCA=∠AOB=90°,∠OAC=∠CAB=30°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=4,则k的值为$\sqrt{3}$.
分析 设OC=a,BD=b,利用含30度的直角三角形三边的关系得到AC=$\sqrt{3}$a,OA=2a,AD=$\sqrt{3}$b,AB=2b,则B(a+b,$\sqrt{3}$a-$\sqrt{3}$b),根据反比例函数图象上点的坐标特征得k=(a+b)($\sqrt{3}$a-$\sqrt{3}$b)=$\sqrt{3}$(a2-b2),再利用OA2-AB2=4得到a2-b2=1,所以k=$\sqrt{3}$.
解答 解:设OC=a,BD=b,
∵Rt△AOC和Rt△ABD,∠OCA=∠AOB=90°,∠OAC=∠CAB=30°,
∴AC=$\sqrt{3}$a,OA=2a,AD=$\sqrt{3}$b,AB=2b,
∴B(a+b,$\sqrt{3}$a-$\sqrt{3}$b),
∵反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,
∴k=(a+b)($\sqrt{3}$a-$\sqrt{3}$b)=$\sqrt{3}$(a2-b2),
∵OA2-AB2=4,
∴4a2-4b2=4,即a2-b2=1,
∴k=$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
18.下列判断错误的是( )
| A. | 多项式5x2-2x+4是二次三项式 | |
| B. | 单项式-a2b3c4的系数是-1,次数是9 | |
| C. | 式子m+5,ab,x=1,-2,$\frac{s}{v}$都是代数式 | |
| D. | 一个有理数不是整数就是分数 |
13.已知一个三角形的两边长分别为4、7,则第三边的长可以为( )
| A. | 2 | B. | 3 | C. | 8 | D. | 12 |
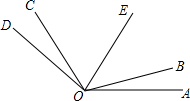 如图,已知OE是∠COA的平分线,∠AOE=59°35′,∠AOB=∠COD=16°17′22″.
如图,已知OE是∠COA的平分线,∠AOE=59°35′,∠AOB=∠COD=16°17′22″. 如图,OC平分∠AOB,OD平分∠AOC,已知∠AOD=15°,则∠BOC=30°.
如图,OC平分∠AOB,OD平分∠AOC,已知∠AOD=15°,则∠BOC=30°. 如图,图形是由一个菱形经过六次旋转得到,每次旋转了60度.
如图,图形是由一个菱形经过六次旋转得到,每次旋转了60度.