题目内容
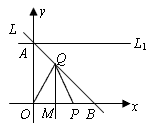
 如图,已知直线l过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为
如图,已知直线l过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为| 9 | 2 |
分析:首先求得直线AB的解析式,然后根据面积求得P点的纵坐标,然后代入求得其横坐标,代入二次函数即可求解.
解答:解:设点P(X,y),直线AB的解析式为y=kx+b,
将A(4,0)、B(0,4)分别代入y=kx+b,
得k=-1,b=4,
故y=-x+4,
∵△AOP的面积为
=
×4×y
∴y=
再把y=
代入y=-x+4,得x=
,
所以P(
,
)
把P(
,
)代入到y=ax2中得:a=
.
将A(4,0)、B(0,4)分别代入y=kx+b,
得k=-1,b=4,
故y=-x+4,
∵△AOP的面积为
| 9 |
| 2 |
| 1 |
| 2 |
∴y=
| 9 |
| 4 |
再把y=
| 9 |
| 4 |
| 7 |
| 4 |
所以P(
| 7 |
| 4 |
| 9 |
| 4 |
把P(
| 7 |
| 4 |
| 9 |
| 4 |
| 36 |
| 49 |
点评:本题考查的是三角形的性质以及二次函数与图象相结合的应用,难度中等.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
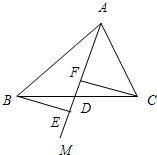 23、如图,已知直线AM过△ABC的边BC的中点D,BE⊥AM于E,CF⊥AM于F.求证:DE=DF.
23、如图,已知直线AM过△ABC的边BC的中点D,BE⊥AM于E,CF⊥AM于F.求证:DE=DF. 如图,已知直线BD过点O,∠AOC=90°,∠COD=125°,则∠AOB=
如图,已知直线BD过点O,∠AOC=90°,∠COD=125°,则∠AOB= 如图,已知直线AM过△ABC的边BC的中点D,BE⊥AM于E,CF⊥AM于F.求证:DE=DF.
如图,已知直线AM过△ABC的边BC的中点D,BE⊥AM于E,CF⊥AM于F.求证:DE=DF.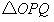 的面积为S,求S关于t的函数关系式;并求出当
的面积为S,求S关于t的函数关系式;并求出当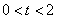 时,S的最大值;
时,S的最大值; 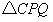 是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.