题目内容

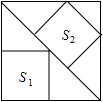如图，一个大正方形中有2个小正方形，如果它们的面积分别是S1，S2，则（　　）
分析：设大正方形的边长为x，根据等腰直角三角形的性质知AC、BC的长，进而可求得S2的边长，由面积的求法可得答案．
解答：解：如图，设大正方形的边长为x，
根据等腰直角三角形的性质知，AC=
2
BC，BC=CE=
2
CD，
∴AC=2CD，CD=
x
3
，
∴S2的边长为
2
3
x，S2的面积为
2
9
x2，S1的边长为
x
2
，S1的面积为
1
4
x2，
∴S1＞S2．
故选A．
点评：本题列出了利用了正方形的性质和等腰直角三角形的性质求解．
练习册系列答案
相关题目
精英家教网如图所示，在一个大正方形中有两个小正方形，它们的面积分别为m、n，则
nm
=
 
．
现有如图1的8张大小形状相同的直角三角形纸片，三边长分别是a、b、c．用其中4张纸片拼成如图2的大正方形（空白部分是边长分别为a和b的正方形）；用另外4张纸片拼成如图3的大正方形（中间的空白部分是边长为c的正方形）．

（一）观察：
从整体看，图2和图3的大正方形的面积都可以表示为（a+b）2，结论①依据整个图形的面积等于各部分面积的和．
图2中的大正方形的面积又可以用含字母a、b的代数式表示为：
a2+b2+2ab
a2+b2+2ab
，结论②
图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为：
c2+2ab
c2+2ab
，结论③
（二）思考：
结合结论①和结论②，可以得到一个等式
（a+b）2=a2+b2+2ab
（a+b）2=a2+b2+2ab
；
结合结论②和结论③，可以得到一个等式
a2+b2=c2
a2+b2=c2
；
（三）应用：
请你运用（二）中得到的结论任意选择下列两个问题中的一个解答：
（1）求1.462+2×1.46×2.54+2.542的值；
（2）若分别以直角三角形三边为直径，向外作半圆（如图4），三个半圆的面积分别记作S1、S2、S3，且S1+S2+S3=20，求S2的值．
（四）延伸（本题作为附加题，做对加2分）
若分别以直角三角形三边为直径，向上作三个半圆（如图5），直角边a=5，b=12，斜边c=13，则表示图中阴影部分面积和的数值是：
A
A
  A．有理数     B．无理数     C．无法判断
请作出选择，并说明理由．

如图，一个大正方形被分割成四个小正方形，沿大正方形的对角线对折，则互相重合的两个小正方形中的数字之积为________．

作业宝如图，一个大正方形中有2个小正方形，如果它们的面积分别是S1，S2，则


  1. A.
    S1＞S2
  2. B.
    S2＞S1
  3. C.
    S1≥S2
  4. D.
    S1=S2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网