题目内容
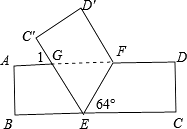
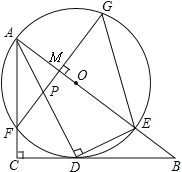
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
【答案】(1)证明见解析;(2)6;(3)![]()
【解析】试题分析:(1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
试题解析:(1)证明:连结OD.∵DE⊥AD,∴AE是⊙O的直径,即O在AE上.
∵AD是角平分线,∴∠1=∠2.
∵OA=OD,∴∠2=∠3.∴∠1=∠3.∴OD∥AC.
∵∠C=90°,∴OD⊥BC.∴BC是⊙O的切线.
(2)解:∵OD∥AC,∴∠4=∠EAF.
∵∠G=∠EAF,∴∠4=∠G.
∴tan∠4=tan∠G=![]() .
.
设BD=4k,则OD=OE=3k.
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+4)2,
解得,k1=2,k2=![]() (舍),(注:也可由OB=5k=3k+4得k=2),
(舍),(注:也可由OB=5k=3k+4得k=2),
∴3k=6,即⊙O的半径为6.
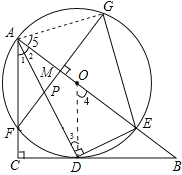
(3)解:连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=![]() ,即
,即![]() ,
, ![]() ,
,
∴![]() ,
,
∴AM=![]() AE=
AE=![]() =
=![]() .
.
∵OD∥AC,∴![]() ,
, ![]() ,即
,即![]() ,
, ![]() .
.
∴AC=![]() ,CD=
,CD=![]() .
.
∵∠1=∠2,∠ACD=∠AMP=90°,∴△ACD∽△AMP.
∴![]() ,∴PM=
,∴PM= ![]() =
=![]() .
.
∴AP=![]() =
=![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目