Question

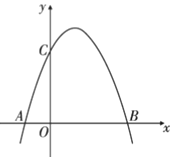
【题目】如图，已知抛物线与轴交于点和点(点在点的左侧)，与轴的交点为.

(1)求点和点的坐标；

(2)若点为抛物线上一点，且，求点的坐标.

Answer 1

【答案】(1)点的坐标分别为，；(2)点的坐标是.

【解析】

（1）当时，解一元二次方程，得到方程的解，即可得到A、B的坐标；

（2）先求出点C坐标，然后得到OB=OC，则，从而得到；根据，对点N进行分析，可分为①当点N在点C的右侧时，②当点N在点C的左侧时两类进行讨论分析，从而通过计算，得到点N的坐标.

解：(1)当时，，

解得：，

∵点在点的左侧，

∴点的坐标分别为，；

(2)连接，在中，令，则.

即的坐标是，.

∵点的坐标是，

∴，

∴，则是等腰直角三角形.

∴.

过点作轴，垂足是.

∵，

∴，

∴，

设点的坐标是，当点在点右侧时，

∴，

∴，

解得：(舍去)或

∴点的坐标是；

当点在点左侧时，

∴，

∴，

解得：(舍去)或(舍去)

综上，点的坐标是.