题目内容
9.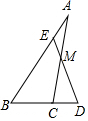 如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=$\frac{1}{4}$AB,连结EM并延长,交BC的延长线于D,此时BC:CD为2:1.
如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=$\frac{1}{4}$AB,连结EM并延长,交BC的延长线于D,此时BC:CD为2:1.
分析 过C点作CP∥AB,交DE于P,由PC∥AE知$\frac{PC}{AE}$=$\frac{CM}{AM}$、且AM=CM,得PC=AE,根据AE=$\frac{1}{4}$AB得CP=$\frac{1}{4}$AB、CP=$\frac{1}{3}$BE,由CP∥BE知$\frac{CP}{BE}$=$\frac{CD}{BD}$=$\frac{1}{3}$,可得BD=3CD,继而得出答案.
解答 解:过C点作CP∥AB,交DE于P,如图,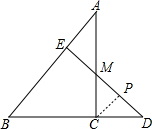
∵PC∥AE,
∴$\frac{PC}{AE}$=$\frac{CM}{AM}$,
而AM=CM,
∴PC=AE,
∵AE=$\frac{1}{4}$AB,
∴CP=$\frac{1}{4}$AB,
∴CP=$\frac{1}{3}$BE,
∵CP∥BE,
∴$\frac{CP}{BE}$=$\frac{CD}{BD}$=$\frac{1}{3}$,
∴BD=3CD,
∴BC=2CD,即BC:CD为2:1,
故答案为:2:1.
点评 本题考查了平行线分线段成比例,掌握三条平行线截两条直线,所得的对应线段成比例是解题的关键.

练习册系列答案
相关题目
15.求1+2+22+23…+22012的值,可令S=1+2+22+23+…+22012,则2S=2+22+23+24+…+22013,因此2S-S=22013-1,仿照以上推理,计算出1+5+52+53+…+52017的值为( )
| A. | 52017-1 | B. | 52018-1 | C. | $\frac{{5}^{2018}-1}{4}$ | D. | $\frac{{5}^{2017}-1}{4}$ |
4.代数式(x-$\frac{3}{2}$)(x+$\frac{2}{3}$)的值为0,则x的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$或-$\frac{2}{3}$ | D. | 0 |
1.为考察小明和小亮的学习成绩,参看了他们上学期期中、期末成绩,如下表所示
根据你的观察小明的成绩较好.
| 成绩 姓名 | 期中 | 期末 |
| 小明 | 92 | 95 |
| 小亮 | 87 | 91 |
 【问题引入】
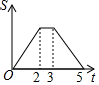
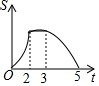
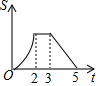
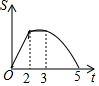
【问题引入】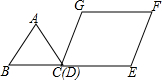 如图,等边△ABC边长为2,四边形DEFG是平行四边形,DG=2,DE=3,∠GDE=60°,BC和DE在同一条直线上,且点C与点D重合,现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动,当点B与点E重合时停止,则在这个运动过程中,△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
如图,等边△ABC边长为2,四边形DEFG是平行四边形,DG=2,DE=3,∠GDE=60°,BC和DE在同一条直线上,且点C与点D重合,现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动,当点B与点E重合时停止,则在这个运动过程中,△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是( )