题目内容
将两块全等的含30°的直角三角尺按如图1摆放在一起,设较短的直角边为1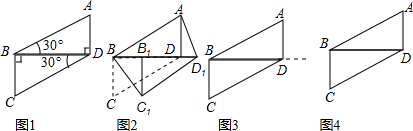
(1)四边形ABCD是平行四边形吗?说出你的结论和理由:
(2)如图2,Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置,问四边形ABC1D1是平行四边形吗?说出你的结论和理由:
(3)如图3,在将Rt△BCD沿射线BD方向平移的过程中,当点B的移动距离为
(4)如图4,在将Rt△BCD沿射线BD方向平移的过程中,四边形ABC1D1恰好为矩形,设点B移动的距离等于x,则x2=
分析:(1)由于图中摆放的两个三角形是全等三角形,那么∠ABD=∠CDB、∠ADB=∠CBD,由此得四边形ABCD的两组对边分别平行,由此可判定四边形ABCD是平行四边形.
(2)可按照(1)的思路进行求解;那么就需要证出BC1∥AD1,即∠AD1B=∠C1BD1,观察图形,证△BB1C1≌△D1DA即可.
(3)若平行四边形ABC1D1是菱形,那么边AB=BC1,即此时△ABD≌△C1BB1,那么BB1=BD,即D、B1重合,此时B点移动的距离为BD的长,即
.
(4)若平行四边形ABC1D1恰好为矩形,那么∠ABC1必为直角,即∠C1BB1=60°,在Rt△C1BB1中,已知了B1C1的长,根据直角三角形的性质即可求得BB1的长,即x的值,进而可得x2的值.
(2)可按照(1)的思路进行求解;那么就需要证出BC1∥AD1,即∠AD1B=∠C1BD1,观察图形,证△BB1C1≌△D1DA即可.
(3)若平行四边形ABC1D1是菱形,那么边AB=BC1,即此时△ABD≌△C1BB1,那么BB1=BD,即D、B1重合,此时B点移动的距离为BD的长,即
| 3 |
(4)若平行四边形ABC1D1恰好为矩形,那么∠ABC1必为直角,即∠C1BB1=60°,在Rt△C1BB1中,已知了B1C1的长,根据直角三角形的性质即可求得BB1的长,即x的值,进而可得x2的值.
解答:解:(1)四边形ABCD是平行四边形;
理由:由于△ABD、△BCD是全等三角形,故∠ABD=∠CDB,∠ADB=∠CBD,即AB∥CD、BC∥AD;
因为两组对边分别平行的四边形是平行四边形,所以四边形ABCD是平行四边形.
(2)四边形ABC1D1是平行四边形;
证明:由题意知:B1C1=AD,BB1=DD1,∠BB1C1=∠ADD1=90°,
∴△ADD1≌△C1B1B,
∴∠AD1B=∠C1BD,即BC1∥AD1;
易知:∠ABD=∠C1D1B,即AB∥C1D1,
∴四边形ABC1D1是平行四边形.
(3)若平行四边形ABC1D1为菱形,则AB=BC1,
又∵B1C1=AD,∠BB1C1=∠ADB=90°,
∴△BC1B1≌△BAD,得BB1=BD,即B1、D重合;
易知BD=
,所以若四边形ABC1D1为菱形,点B需要移动
个单位长度;
理由是:一组邻边相等的平行四边形是菱形.
(4)若平行四边形ABC1D1为矩形,则∠ABC1=90°,∠B1BC1=60°;
Rt△BB1C1中,B1C1=1,若∠B1BC1=60°,则BB1=
;
故x2=(
)2=
.
理由:由于△ABD、△BCD是全等三角形,故∠ABD=∠CDB,∠ADB=∠CBD,即AB∥CD、BC∥AD;
因为两组对边分别平行的四边形是平行四边形,所以四边形ABCD是平行四边形.
(2)四边形ABC1D1是平行四边形;
证明:由题意知:B1C1=AD,BB1=DD1,∠BB1C1=∠ADD1=90°,
∴△ADD1≌△C1B1B,
∴∠AD1B=∠C1BD,即BC1∥AD1;
易知:∠ABD=∠C1D1B,即AB∥C1D1,
∴四边形ABC1D1是平行四边形.
(3)若平行四边形ABC1D1为菱形,则AB=BC1,
又∵B1C1=AD,∠BB1C1=∠ADB=90°,
∴△BC1B1≌△BAD,得BB1=BD,即B1、D重合;
易知BD=
| 3 |
| 3 |
理由是:一组邻边相等的平行四边形是菱形.
(4)若平行四边形ABC1D1为矩形,则∠ABC1=90°,∠B1BC1=60°;
Rt△BB1C1中,B1C1=1,若∠B1BC1=60°,则BB1=
| ||
| 3 |
故x2=(
| ||
| 3 |
| 1 |
| 3 |
点评:此题主要考查了全等三角形的性质,平行四边形、菱形和矩形的判定等知识,难度不大.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
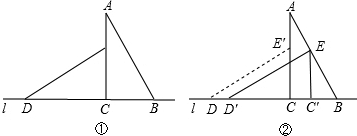
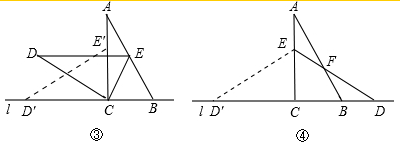
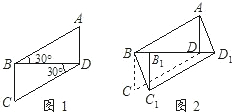
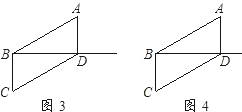
 活用知识,解决问题.
活用知识,解决问题.
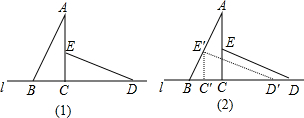 )的位置,使E点落在AB上,则CC′=( )
)的位置,使E点落在AB上,则CC′=( )