题目内容
已知AD是△ABC的中线，∠C=90°，DE⊥AB于点E，试说明AC2=AE2-BE2．
证明：∵AD是△ABC的中线，
∴BD=CD．
∵∠C=90°，DE⊥AB于E，
∴AE2-BE2=（AD2-DE2）-（BD2-DE2）=AD2-BD2=AD2-CD2=AC2．
故AC2=AE2-BE2．
分析：根据直角三角形的性质和勾股定理可得AE2-BE2=（AD2-DE2）-（BD2-DE2）=AD2-BD2=AD2-CD2=AC2，从而证明结论．
点评：考查了直角三角形的性质和勾股定理，注意线段相互间的转化．
∴BD=CD．
∵∠C=90°，DE⊥AB于E，
∴AE2-BE2=（AD2-DE2）-（BD2-DE2）=AD2-BD2=AD2-CD2=AC2．
故AC2=AE2-BE2．
分析：根据直角三角形的性质和勾股定理可得AE2-BE2=（AD2-DE2）-（BD2-DE2）=AD2-BD2=AD2-CD2=AC2，从而证明结论．
点评：考查了直角三角形的性质和勾股定理，注意线段相互间的转化．
练习册系列答案
相关题目
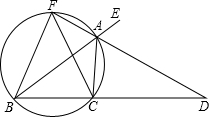于点F，连接FB、FC．
3、如图，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：①AG：AD=1：2；②GE：BE=1：4；③GE：BE=3：4，其中正确的为（ ）
