题目内容
因式分解:2x2-5xy+2y2+7x-5y+3.
考点:因式分解-分组分解法
专题:计算题
分析:原式结合后,利用十字相乘法分解即可.
解答:解:2x2-5xy+2y2-7x+5y+3
=2x2-(5y+7)x+(2y2+5y+3)
=2x2-(5y+7)x+(y+1)(2y+3)
=(2x-y-1)(x-2y-3).
=2x2-(5y+7)x+(2y2+5y+3)
=2x2-(5y+7)x+(y+1)(2y+3)
=(2x-y-1)(x-2y-3).
点评:此题考查了因式分解-分组分解法,进行适当的分组是解本题的关键.

练习册系列答案
相关题目
若关于x的方程
-1=0有增根,求a的值( )
| ax+1 |
| x-1 |
| A、0 | B、-1 | C、1 | D、-2 |
已知x2-4xy+4y2=0,则分式
的值为( )
| x-y |
| x+y |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
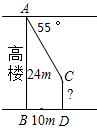 如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于
如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于 如图,以DE为轴,折叠等边△ABC,顶点A正好落在BC边上F点,求证:△DBF∽△FCE.
如图,以DE为轴,折叠等边△ABC,顶点A正好落在BC边上F点,求证:△DBF∽△FCE.