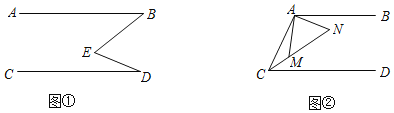题目内容
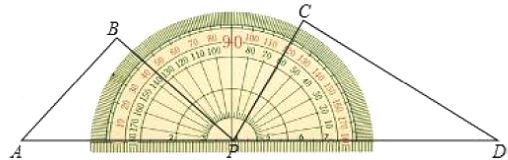
【题目】已知:![]() 为直线
为直线 ![]() 上的一点,以
上的一点,以![]() 为观察中心,射线
为观察中心,射线![]() 表示正北方向,
表示正北方向,![]() 表示正东方向(即
表示正东方向(即![]() ),射线
),射线![]() ,射线
,射线![]() 的方向如各图所示.
的方向如各图所示.
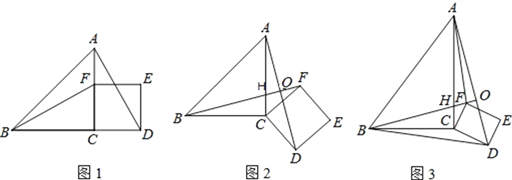
(1)如图1所示,当 ![]() 时:
时:
①若![]() ,则射线
,则射线![]() 的方向是 .
的方向是 .
② ![]() 与
与![]() 的关系为 ,
的关系为 ,
③ ![]() 与
与![]() 的关系为 .
的关系为 .
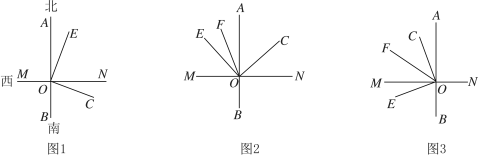
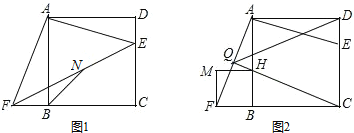
(2)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,另一条射线
的位置,另一条射线![]() 恰好平分
恰好平分![]() ,旋转中始终保持
,旋转中始终保持![]() .
.
①若![]() ,则
,则![]() 度 .
度 .
②若![]() ,则
,则![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
(3)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,射线
的位置,射线![]() 仍然平分
仍然平分![]() ,旋转中始终保持
,旋转中始终保持![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系,并说明理由.
之间存在怎样的数量关系,并说明理由.
【答案】(1)①北偏东20°;②相等;③互补.(2)①24°;②2β.(3)∠CON=2∠AOF,理由见解析.
【解析】
(1)①根据方向角的定义即可求解;②根据同角的余角相等即可得出结论;③先根据同角的余角相等得出∠EON=∠BOC,再根据两角互补的定义即可得出结果.
(2)①根据同角的余角可知∠AOC=∠MOE,又根据角平分线的定义可得∠COF=∠MOF,两式相减即可得出结果.②由①知∠AOF=∠EOF=β,又由∠CON=∠AOE即可得出结果.
(3)根据角的和差,以及角平分线的定义即可求解.
解:(1)①北偏东20°
②∵由题意知,∠AOE+∠EON=90°,∠NOC+∠EON=90°,
∴∠AOE=∠CON.
③由题意知,∠BOC+∠NOC=90°,∠NOC+∠EON=90°,
∴∠BOC=∠EON,
又∠AOC+∠BOC=180°,
∴∠AOC+∠EON=180°.
故答案为:①北偏东20°;②相等;③互补.
(2)①由题意知,∠AOC+∠AOE=90°,∠MOE+∠AOE=90°,
∴∠AOC=∠MOE,
又OF为∠COM的角平分线,
∴∠COF=∠MOF,
∴∠COF-∠AOC =∠MOF-∠MOE,
∴∠AOF=∠EOF=24°.
②由①知,∠AOF=∠EOF=β,
∴∠CON=∠AOE=2∠AOF=2β.
故答案为:①24°;②2β.
(3)∵∠CON=180°-∠COM=180°-2∠MOF.
又∠AOF=90°-∠MOF,∴2∠AOF=180°-2∠MOF.
∴∠CON=2∠AOF.

 三点一测快乐周计划系列答案
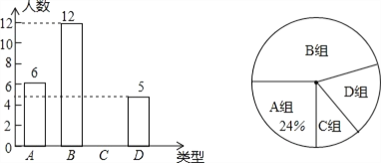
三点一测快乐周计划系列答案【题目】王老师为了了解学生在数学学习中的纠错情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年级(5)班和八年级(6)班进行了检测.并从两班各随机抽取10名学生的得分绘制成下列两个统计图.根据以上信息,整理分析数据如下:
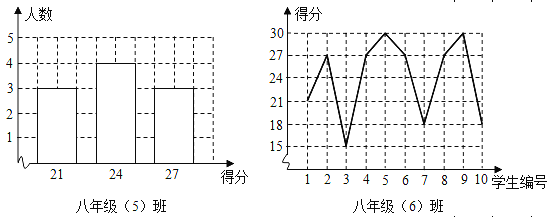
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年级(5)班 | a | 24 | 24 |
八年级(6)班 | 24 | b | c |
(1)求出表格中a,b,c的值;
(2)你认为哪个班的学生纠错得分情况比较整齐一些,通过计算说明理由.