题目内容
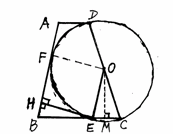
如图所示,在等腰梯形ABCD中,AD∥BC,O为CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E,过E作EH⊥AB于H,已知⊙O与AB边相切于F。
(1)求证:OE∥AB。(4分)
(2)求证:EH=![]() AB。(3分)
AB。(3分)
(3)已知![]() ,求
,求![]() 的值。(3分)
的值。(3分)

(1)(4分)证明:∵ABCD为等腰梯形且AD//BC ∴∠B=∠C ∵OE=OC ∴∠C=∠OEC
∴∠OEC=∠B ∴OE//AB
(2)(3分)证明:连结FO,∵AB切 ⊙O于F ∴AB⊥FO ∵EH⊥AB,OE//AB
∴OE⊥EH ∴OFHE为矩形 ∵OE=OF ∴OFHE为正方形 ∴EH=EO
∵O为CD中点,OC为⊙O半径, ∴CD为⊙O直径 ∴EO=![]() CD ∴EH=
CD ∴EH=![]() CD
CD
∵ABCD为等腰梯形 ∴CD=AB ∴EH=![]() AB
AB
(3)(3分)解:作OM⊥BC于点M,∵EH⊥AB,OM⊥BC ∴∠BHE=∠OME=90°
∵∠OEC=∠B ∴△BHE∽△EMO ∴![]() ∴
∴![]()
∵EO=CO, OM⊥BC ∴EM=![]() CE ∴
CE ∴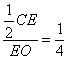 ∴CE=
∴CE=![]()
∵![]() ∴可设BH=K,BE=4K 在Rt△BHE中有:HE=
∴可设BH=K,BE=4K 在Rt△BHE中有:HE=![]()
∵HE=EO ∴![]() ∴
∴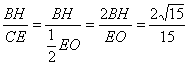

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE.
1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE. 48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.
48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.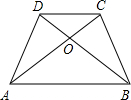 如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为
如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为 如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°
如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°