题目内容
 已知,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
已知,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.(1)判断△ACD的形状?并说明理由.
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
考点:命题与定理,直角三角形的性质
专题:
分析:(1)根据∠ACB=90°,得出∠A+∠B=90°,根据∠ACD=∠B,得出∠A+∠ACD=90°,再根据两锐角互余的三角形是直角三角形即可得出答案,
(2)根据证明过程可得应用了直角三角形的两锐角互余,两锐角互余的三角形是直角三角形,这一对互逆的真命题.
(2)根据证明过程可得应用了直角三角形的两锐角互余,两锐角互余的三角形是直角三角形,这一对互逆的真命题.
解答:解:(1)∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴△ACD是直角三角形;
(2)应用了直角三角形的两锐角互余,两锐角互余的三角形是直角三角形,这一对互逆的真命题.
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴△ACD是直角三角形;
(2)应用了直角三角形的两锐角互余,两锐角互余的三角形是直角三角形,这一对互逆的真命题.
点评:此题考查了命题与定理,用到的知识点是直角三角形的性质和判定、互逆命题、真命题,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
下列运算正确的是( )
| A、4a3÷2a=2a3 |
| B、(3a2)2=6a4 |
| C、ab+ba=2ab |
| D、(-3a+2)(3a-2)=9a2-4 |
 一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?
一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?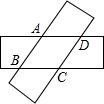 如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由.
如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.