题目内容
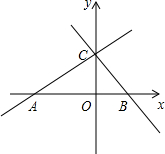 如图,在平面直角坐标系中.点O为坐标原点,直线y=
如图,在平面直角坐标系中.点O为坐标原点,直线y=| 3 |
| 4 |
(1)求直线BC的解析式;
(2)连接EF,将射线EF绕点E顺时针旋转45°,交直线BC于点Q,过点F作FM⊥EQ,垂足为M,连接MC,求MC的长;
(3)在(2)的条件下,t为何值时FC=
| 1 |
| 5 |
考点:一次函数综合题
专题:
分析:(1)根据y=
x+6与x轴交于点A,与y轴交于点C,求出OA=8,OC=6,设OB=a,根据
=
,求出a,得出点B的坐标,再把B、C两点的坐标代入y=kx+b即可得出答案;
(2)过点M作MK⊥FC交AC于点K,根据∠EMK=∠FMC,∠FEM=∠MCF,ME=MF,证出△MEK≌△MFC,得出∠MCK=∠MKC=45°,再求出AC=10,BC=
,从而得出CE=10-t,CF=
-t,再求出CK=CE-EK=
,最后根据
CM=CK,即可得出CM的长;
(3)以CA,CB分别为x 轴、y 轴建立直角坐标系,则A(10,0),B(0,
),E(10+t,0),F(0,
-t),求得EF的斜率k1=
=
,又知EQ到EF的角为 45°,求得EQ的斜率k2 满足 tan45°=
=1,即k2=
=
=
令Q(0,h)又有k2=
=
,解之得h=
,由CQ=6CF,则
=6(
-t) 整理得24t2-115t+125=0即可解得.
| 3 |
| 4 |
| OC |
| OA |
| OB |
| OC |
(2)过点M作MK⊥FC交AC于点K,根据∠EMK=∠FMC,∠FEM=∠MCF,ME=MF,证出△MEK≌△MFC,得出∠MCK=∠MKC=45°,再求出AC=10,BC=
| 15 |
| 2 |
| 15 |
| 2 |
| 35 |
| 2 |
| 2 |
(3)以CA,CB分别为x 轴、y 轴建立直角坐标系,则A(10,0),B(0,
| 15 |
| 2 |
| 15 |
| 2 |
t-
| ||
| t+10 |
| 2t-15 |
| 2t+20 |
| k1-k2 |
| 1+k1k2 |
| k1-1 |
| k2+1 |
| ||
|
| -35 |
| 4t+5 |
| h |
| -10-t |
| -35 |
| 4t+5 |
| 350+35t |
| 4t+5 |
| 350+35t |
| 4t+5 |
| 15 |
| 2 |
解答:解:(1)∵y=
x+6与x轴交于点A,与y轴交于点C,
∴A(-8,0),C(0,6),
∴OA=8,OC=6,
设OB=a,
∵∠CAB=∠OCB,
∴tan∠CAB=tan∠OCB,
∴
=
=
,
∴
=
,
∴a=
∴B(
,0),
设直线BC的解析式为y=kx+b,
把B、C两点的坐标代入y=kx+b得:
,
解得:
,
∴直线BC的解析式为y=-
x+6;
(2)过点M作MK⊥MC交AC于点K,
∵∠EMF=∠KMC=90°,
∴∠EMK=∠FMC,
∵∠CAB=∠OCB
∴∠CAB+∠ACO=∠OCB+∠ACO=90°
∴∠ACB=90°,
∵∠CKM+∠KCM=∠KCM+∠MCF=90°
∴∠CKM=∠MCF,
∵∠MEF=∠45°,FM⊥EM,
∴EM=FM
在△MEK和△MFC中,
∴△MEK≌△MFC(AAS),
∴EK=CF MK=MC,
∴∠MCK=∠MKC=45°,
∵OC=6,OA=8,OB=
,
∴AC=10,BC=
,
∴CE=10+t,CF=
-t,
∴CK=CE+EK=10+t+(
-t)=
,
∴
CM=CK=
,
∴CM=
.

(3)在(2)的条件下,t=
或
时,FC=
FQ

| 3 |
| 4 |
∴A(-8,0),C(0,6),
∴OA=8,OC=6,
设OB=a,
∵∠CAB=∠OCB,
∴tan∠CAB=tan∠OCB,
∴
| OC |
| OA |
| OB |
| OC |
| 6 |
| 8 |
∴
| 6 |
| 8 |
| a |
| 6 |
∴a=
| 9 |
| 2 |
∴B(
| 9 |
| 2 |
设直线BC的解析式为y=kx+b,
把B、C两点的坐标代入y=kx+b得:
|
解得:
|
∴直线BC的解析式为y=-
| 4 |
| 3 |
(2)过点M作MK⊥MC交AC于点K,
∵∠EMF=∠KMC=90°,
∴∠EMK=∠FMC,
∵∠CAB=∠OCB
∴∠CAB+∠ACO=∠OCB+∠ACO=90°
∴∠ACB=90°,
∵∠CKM+∠KCM=∠KCM+∠MCF=90°
∴∠CKM=∠MCF,
∵∠MEF=∠45°,FM⊥EM,
∴EM=FM
在△MEK和△MFC中,
|
∴△MEK≌△MFC(AAS),
∴EK=CF MK=MC,
∴∠MCK=∠MKC=45°,
∵OC=6,OA=8,OB=
| 9 |
| 2 |
∴AC=10,BC=
| 15 |
| 2 |
∴CE=10+t,CF=
| 15 |
| 2 |
∴CK=CE+EK=10+t+(
| 15 |
| 2 |
| 35 |
| 2 |
∴
| 2 |
| 35 |
| 2 |
∴CM=
35
| ||
| 4 |

(3)在(2)的条件下,t=
| 5 |
| 3 |
| 25 |
| 8 |
| 1 |
| 5 |

点评:本次考查的是一次函数的综合应用,用的知识点是一次函数的图象和性质、全等三角形的全等与性质,解题时注意分类讨论思想的应用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数为( )
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数为( )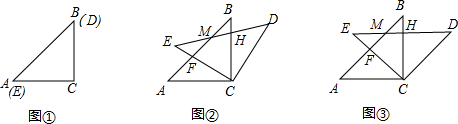
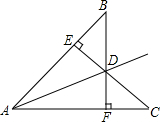 如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且AD平分∠BAC.
如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且AD平分∠BAC.