题目内容
写出一个你喜欢的实数k的值: ,使得反比例函数y=
的图象在每一个象限内y都随x的增大而增大.
| 1-k |
| x |
考点:反比例函数的性质
专题:开放型
分析:根据反比例函数的性质得出关于k的不等式,求出k的取值范围,在此取值范围内找出一个符合条件的k的值即可.
解答:解:∵反比例函数y=
的图象在每一个象限内,y随x的增大而增大,
∴1-k<0,解得k>1.
∴k可以为:2(答案不唯一).
故答案为:2(答案不唯一).
| 1-k |
| x |
∴1-k<0,解得k>1.
∴k可以为:2(答案不唯一).
故答案为:2(答案不唯一).
点评:本题考查的是反比例函数的性质,根据题意得出关于k的不等式,求出k的取值范围是解答此题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
下列语句正确的是( )
| A、连接两点的线段叫做两点间的距离 |
| B、两条直线平行,对顶角相等 |
| C、如果两个角互补,那么这两个角为邻补角 |
| D、平移变换中,各组对应点连成的线段平行且相等 |
代数式
+
+
的所有可能的值有( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、无数个 |
若两圆外切,半径分别为4和7,则它们的圆心距是( )
| A、2 | B、3 | C、6 | D、11 |
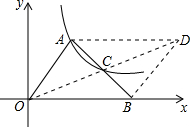 如图,在平行四边形OADB中,对角线AB、OD相交于点C,反比例函数y=
如图,在平行四边形OADB中,对角线AB、OD相交于点C,反比例函数y= 如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB=
如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB=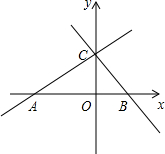 如图,在平面直角坐标系中.点O为坐标原点,直线y=
如图,在平面直角坐标系中.点O为坐标原点,直线y=