题目内容
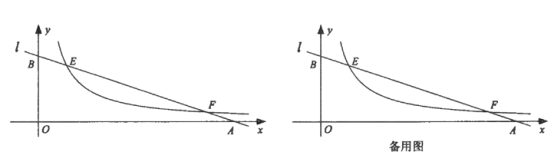
【题目】如图，直线l的解析式为y=-
x+
，与x轴，y轴分别交于A，B两点，双曲线
与直线l交于E，F两点，点E的横坐标为1.
(1)求k的值及F点的坐标;
(2)连接OE，OF，求△EOF的面积;
(3)若点P是EF下方双曲线上的动点(不与E，F重合)，过点P作x轴，y轴的垂线，分别交直线l于点M，N，求
的值.
【答案】（1）
；（2）
；（3）
【解析】
（1）求出点E纵坐标，把点E坐标代入反比例函数解析式中即可求出k的值，再联立方程组求出点F的坐标；
（2）运用“割补法”，根据
求解即可；
（1）设点
的坐标为（1，a），代入y= y=-
x+
得，a=2,
∴
,
把代入
得
，
∴
联立方程组得
，解得
，
∴
（2）分别过点、
做
轴的垂线段
、
，如图，
令y=0,则
，解得x=7，令x=0，则y=
∴
，
，
又，，
∵
=
=
=
（3）如图，
设
，则有
则
，
，，
∴
，
∴
练习册系列答案
名校课堂系列答案
相关题目
