题目内容
如图,已知线段AB∥CD,AD与B C相交于点K,E是线段AD上一动点.
【小题1】若BK=
 KC,求
KC,求 的值
的值【小题2】连接BE,若BE平分∠ABC,则当AE=
 AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明【小题3】再探究:当AE=
 AD(
AD( ),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
p;【答案】
【小题1】∵AB∥CD,∴∠KAB=∠KDC,又∵∠AKB=DKC,
∴△AKB∽△DKC,………………………………………………………………2分
∴ .……………………………………………………4分
.……………………………………………………4分
【小题2】猜想:AB=BC+CD.……………………………………………………5分
证明:分别延长BE、DC相交于点F.
∵AB∥DF,∴∠ABE=∠DFE,
∵AE= AD,∴AE=ED,
AD,∴AE=ED,
又∵∠AEB=∠DEF,∴△AEB≌△DEF,…………………………………………6分
∴AB=DF,
∵BE平分∠ABC,即∠ABE=∠EBC,
∴∠CFE=∠EBC,∴FC=BC,……………………………………………………7分
∴AB=FD=FC+CD=BC+CD.……………………………………………………8分
【小题3】当AE= AD(
AD( )时,线段AB、BC、CD三者之间又有怎样的等量关系为:
)时,线段AB、BC、CD三者之间又有怎样的等量关系为:
 (
( ).…………………………………………………10分解析:
).…………………………………………………10分解析:
(1)先证明△AKB∽△DKC,然后根据相似三角形对应边成比例得出 的值;
的值;
(2)把BC和CD转化到一直线上,然后用三角形全等来证明对应边相等从而得出结论;
(3)同(2)思路相同,不过证明二个三角形相似,然后通过对应边成比例得出线段AB、BC、CD三者之间等量关系
【小题1】∵AB∥CD,∴∠KAB=∠KDC,又∵∠AKB=DKC,
∴△AKB∽△DKC,………………………………………………………………2分
∴
 .……………………………………………………4分
.……………………………………………………4分【小题2】猜想:AB=BC+CD.……………………………………………………5分
证明:分别延长BE、DC相交于点F.
∵AB∥DF,∴∠ABE=∠DFE,
∵AE=
 AD,∴AE=ED,
AD,∴AE=ED,又∵∠AEB=∠DEF,∴△AEB≌△DEF,…………………………………………6分
∴AB=DF,
∵BE平分∠ABC,即∠ABE=∠EBC,
∴∠CFE=∠EBC,∴FC=BC,……………………………………………………7分
∴AB=FD=FC+CD=BC+CD.……………………………………………………8分
【小题3】当AE=
 AD(
AD( )时,线段AB、BC、CD三者之间又有怎样的等量关系为:
)时,线段AB、BC、CD三者之间又有怎样的等量关系为: (
( ).…………………………………………………10分解析:
).…………………………………………………10分解析:(1)先证明△AKB∽△DKC,然后根据相似三角形对应边成比例得出
 的值;
的值;(2)把BC和CD转化到一直线上,然后用三角形全等来证明对应边相等从而得出结论;
(3)同(2)思路相同,不过证明二个三角形相似,然后通过对应边成比例得出线段AB、BC、CD三者之间等量关系

练习册系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


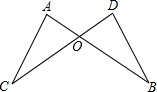 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.