题目内容
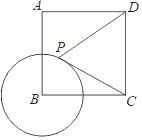
【题目】小明研究了这样一道几何题:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,请问
时,请问![]() 边
边![]() 上的中线
上的中线![]() 与
与![]() 的数量关系是什么?以下是他的研究过程:
的数量关系是什么?以下是他的研究过程:
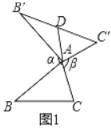
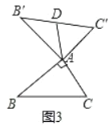
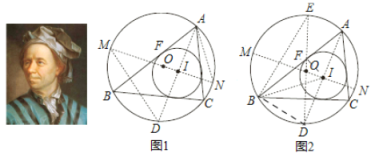
特例验证:(1)①如图2,当![]() 为等边三角形时,猜想
为等边三角形时,猜想![]() 与
与![]() 的数量关系为
的数量关系为![]() _______
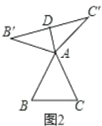
_______![]() ;②如图3,当
;②如图3,当![]() ,
,![]() 时,则
时,则![]() 长为________.
长为________.
猜想论证:(2)在图1中,当![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
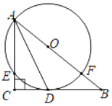
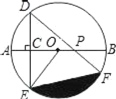
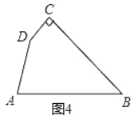
拓展应用:(3)如图4,在四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,在四边形内部是否存在点
,在四边形内部是否存在点![]() ,使
,使![]() 与
与![]() 之间满足小明探究的问题中的边角关系?若存在,请画出点
之间满足小明探究的问题中的边角关系?若存在,请画出点![]() 的位置(保留作图痕迹,不需要说明)并直接写出
的位置(保留作图痕迹,不需要说明)并直接写出![]() 的边
的边![]() 上的中线
上的中线![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
【答案】(1)①![]() ;②4,(2)
;②4,(2)![]() ;理由见解析,(3)存在;
;理由见解析,(3)存在;![]()
【解析】
(1)①首先证明![]() 是含有
是含有![]() 的直角三角形,可得
的直角三角形,可得![]() ,即可解决问题;②首先证明
,即可解决问题;②首先证明![]() ,根据直角三角形斜边中线定理即可解决问题.
,根据直角三角形斜边中线定理即可解决问题.
(2)![]() 与
与![]() 的数量关系为
的数量关系为![]() ,如图5,延长
,如图5,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,先证四边形
,先证四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() ,即可解决问题.
,即可解决问题.
(3)存在,如图6,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,做直线
,做直线![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,作
,作![]() 的中线
的中线![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,先证明
,先证明![]() ,
,![]() ,再证明
,再证明![]() ,即可得出结论,再在
,即可得出结论,再在![]() 中,根据勾股定理,即可求出
中,根据勾股定理,即可求出![]() 的长.
的长.
(1)①如图2,∵![]() 是等边三角形,把
是等边三角形,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 边
边![]() 上的中线,∴
上的中线,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
故答案为:![]() .
.
②如图3,∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() 和
和![]() 为直角三角形,
为直角三角形,
∵把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中,
中,
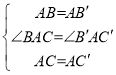
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 边
边![]() 上的中线,
上的中线,![]() 为直角三角形,
为直角三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
故答案为:![]() .
.
(2)![]() ,
,
如图5,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,
,
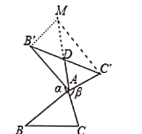
图5
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴在![]() 和
和![]() 中,
中,
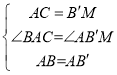
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)存在,
如图6,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,作直线
,作直线![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,作
,作![]() 的中线
的中线![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
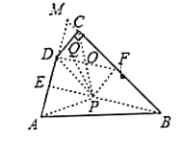
图6
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 之间满足小明探究的问题中的边角关系,
之间满足小明探究的问题中的边角关系,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.

 高效智能课时作业系列答案
高效智能课时作业系列答案