Question

如图：在?ABCD中，AC为其对角线，过点D作AC的平行线与BC的延长线交于E．

（1）求证：△ABC≌△DCE；

（2）若AC=BC，求证：四边形ACED为菱形．

 

 

Answer 1

（1）证明见解析

（2）证明见解析

【解析】

试题分析：（1）由AAS即可判定两三角形全等；

（2）首先证得四边形ACED为平行四边形，然后证得AC=AD，利用邻边相等的平行四边形是菱形判定即可．

试题解析：（1）∵四边形ABCD为平行四边形，

∴AB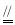CD，∠B=∠ADC，

∴∠B=∠DCE，

又∵DE∥AC

∴∠ACB=∠E，

∴△ABC≌△DCE；

（2）∵四边形ABCD为平行四边形

∴AD∥BC，

即AD∥CE，

由DE∥AC，

∴四边形ACED为平行四边形，

∵AC=BC，

∴∠B=∠CAB，

∵AB∥CD，

∴∠CAB=∠ACD，

又∵∠B=∠ADC，

∴∠ADC=∠ACD，

∴AC=AD，

∴平行四边形ACED为菱形．

考点：1、全等三角形的判定与性质；2、平行四边形的性质；3、菱形的判定