题目内容
4．如图所示，在边长为a的正方形中减去一个边长为b的小正方形（a＞b），把剩下的部分拼成 一个梯形．（1）分别计算这两个图形阴影部分的面积；
（2）这个题从几何角度证明的哪个公式？
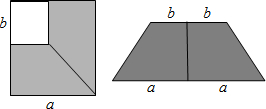
分析 （1）先用大正方形的面积减去小正方形的面积，即可求出S1，再根据梯形的面积公式即可求出S2．
（2）根据（1）得出的值，直接可写出乘法公式（a+b）（a-b）=a2-b2．
解答 解：（1）∵大正方形的边长为a，小正方形的边长为b，
∴S1=a2-b2，
S2=$\frac{1}{2}$（2a+2b）（a-b）=（a+b）（a-b）；
（2）根据题意得：（a+b）（a-b）=a2-b2．
点评 此题考查了平方差公式的几何背景，根据正方形的面积公式和梯形的面积公式得出它们之间的关系是解题的关键，是一道基础题．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
15．
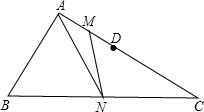如图，在△ABC中，∠BAC=90°，点D在边AC上，AB=CD，点M、N分别为AD、BC的中点，连接MN、AN，MN=3$\sqrt{2}$，AD=4，则线段AN的长为$\sqrt{34}$．
如图，在△ABC中，∠BAC=90°，点D在边AC上，AB=CD，点M、N分别为AD、BC的中点，连接MN、AN，MN=3$\sqrt{2}$，AD=4，则线段AN的长为$\sqrt{34}$．
19．在一个不透明的口袋中装有颜色不同的1个蓝球，2个白球，3个红球，4个黄球，从中任意摸出1个红球的概率是（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
