题目内容
58、如图所示，点E是?ABCD的对角线AC上任意一点，则S△BEC=S△DEC是否正确？请说明理由．分析：S△BEC=S△DEC的底边相等，所以只要证明两三角形的高相等就是了，这就需要作辅助线高，然后利用全等三角形证明即可．当然还有其它作法，比如下图．
解答：
解：S△BEC=S△DEC正确；
连接BD交AC于点O．
∵?ABCD中，BO=DO，
∴S△BOC=S△DOC，S△BOE=S△DOE．
又∵S△BEC=S△BOC+S△BOE，S△DEC=S△DOC+S△DOE，
∴S△BEC=S△DEC
解：S△BEC=S△DEC正确；连接BD交AC于点O．
∵?ABCD中，BO=DO，
∴S△BOC=S△DOC，S△BOE=S△DOE．
又∵S△BEC=S△BOC+S△BOE，S△DEC=S△DOC+S△DOE，
∴S△BEC=S△DEC
点评：此题的关键是证明三角形的底和高相等，当底和高相等时他们的面积就相等．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
反比例数
如图所示，点P是反比例函数y=| k |
| x |
A、y=-
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
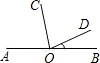如图所示，点O是直线AB上的点，OC平分∠AOD，∠BOD=30°，则∠AOC=
如图所示：点A是反比例函数y=
如图所示，点E是∠AOB的平分线上的一点，EC⊥OA，ED⊥OB，垂足分别为C、D，则下列结论中，错误的是（ ）