题目内容
【题目】如图,已知半圆⊙O的直径AB=10,弦CD∥AB,且CD=8,E为弧CD的中点,点P在弦CD上,联结PE,过点E作PE的垂线交弦CD于点G,交射线OB于点F.
(1)当点F与点B重合时,求CP的长;
(2)设CP=x,OF=y,求y与x的函数关系式及定义域;
(3)如果GP=GF,求△EPF的面积.
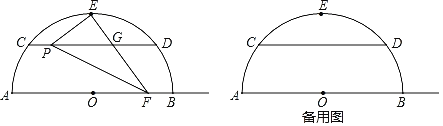
【答案】(1)CP=2;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图1,连接EO,交弦CD于点H,根据垂径定理得EO⊥AB,由勾股定理计算![]() ,可得EH的长,证明∠HPE=∠HGE=45°,则PE=GE.从而可得结论;
,可得EH的长,证明∠HPE=∠HGE=45°,则PE=GE.从而可得结论;
(2)如图2,连接OE,证明△PEH∽△EFO,列比例式可得结论;
(3)如图3,作PQ⊥AB,分别计算PE和EF的长,利用三角形面积公式可得结论.
(1)连接EO,交弦CD于点H,

∵E为弧CD的中点,
∴EO⊥AB,
∵CD∥AB,
∴OH⊥CD,
∴CH=![]() ,
,
连接CO,
∵AB=10,CD=8,
∴CO=5,CH=4,
∴![]() ,
,
∴EH=EO﹣OH=2,
∵点F与点B重合,
∴∠OBE=∠HGE=45°,
∵PE⊥BE,
∴∠HPE=∠HGE=45°,
∴PE=GE,
∴PH=HG=2,
∴CP=CH﹣PH=4﹣2=2;
(2)如图2,连接OE,交CD于H,
∵∠PEH+∠OEF=90°,∠OFE+∠OEF=90°,

∴∠PEH=∠OFE,
∵∠PHE=∠EOF=90°,
∴△PEH∽△EFO,
∴![]() ,
,
∵EH=2,FO=y,PH=4﹣x,EO=5,
∴![]() ,
,
∴![]() .
.
(3)如图3,过点P作PQ⊥AB,垂足为Q,

∵GP=GF,
∴∠GPF=∠GFP,
∵CD∥AB,
∴∠GPF=∠PFQ,
∵PE⊥EF,
∴PQ=PE,
由(2)可知,△PEH∽△EFO,
∴![]() ,
,
∵PQ=OH=3,
∴PE=3,
∵EH=2,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
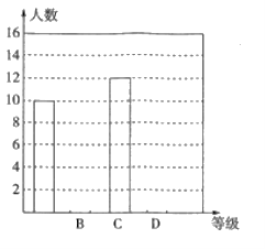
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?