题目内容
若一次函数y=(2m-1)x+3-2m的图象满足y随x的增大而减小,同时交y轴于正半轴,则m的取值范围为
- A.m<2
- B.m<

- C.
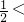 m<
m<
- D.m<

C
分析:根据一次函数图象的增减性和与y轴交点的位置列出关于m的不等式组,通过解该不等式组来求m的取值范围.
解答:∵一次函数y=(2m-1)x+3-2m的图象满足y随x的增大而减小,同时交y轴于正半轴,
∴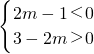 ,
,
解得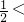 m<
m< .
.
故选C.
点评:函数值y随x的增大而减小?k<0;函数值y随x的增大而增大?k>0;
一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.
分析:根据一次函数图象的增减性和与y轴交点的位置列出关于m的不等式组,通过解该不等式组来求m的取值范围.
解答:∵一次函数y=(2m-1)x+3-2m的图象满足y随x的增大而减小,同时交y轴于正半轴,
∴
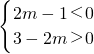 ,
,解得
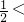 m<
m< .
.故选C.
点评:函数值y随x的增大而减小?k<0;函数值y随x的增大而增大?k>0;
一次函数y=kx+b图象与y轴的正半轴相交?b>0,一次函数y=kx+b图象与y轴的负半轴相交?b<0,一次函数y=kx+b图象过原点?b=0.

练习册系列答案
相关题目