题目内容
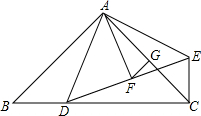 如图在△ABC中,AB=AC,∠BAC=90°,D是BC上的一点,EC⊥BC,EC=BD
如图在△ABC中,AB=AC,∠BAC=90°,D是BC上的一点,EC⊥BC,EC=BD(1)证明:△ABD≌△ACE;
(2)证明:AD⊥AE;
(3)若AF⊥DE,F为垂足,AG=GC,则FG与AC有怎样的位置关系,请说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等腰直角三角形的性质可得∠B=∠ACB=45°,再求出∠ACE=45°,从而得到∠B=∠ACE,再利用“边角边”证明△ABD和△ACE全等;
(2)根据全等三角形对应角相等可得∠BAD=∠CAE,再求出∠DAE=∠BAC,然后根据垂直的定义证明即可;
(3)连接CF,根据全等三角形对应边相等可得AD=AE,根据等腰直角三角形的性质可得AF=DF=EF=
DE,再根据直角三角形斜边上的中线等于斜边的一半可得CF=
DE,从而得到AF=CF,再根据等腰三角形三线合一的性质解答.
(2)根据全等三角形对应角相等可得∠BAD=∠CAE,再求出∠DAE=∠BAC,然后根据垂直的定义证明即可;
(3)连接CF,根据全等三角形对应边相等可得AD=AE,根据等腰直角三角形的性质可得AF=DF=EF=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵EC⊥BC,
∴∠BCE=90°,
∴∠ACE=90°-45°=45°,
∴∠B=∠ACE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)证明:∵△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠DAE=∠CAD+∠CAE=∠CAD+∠BAD=∠BAC=90°,
∴AD⊥AE;
(3)解:FG⊥AC.
理由如下:连接CF,∵△ABD≌△ACE,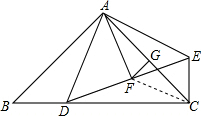
∴AD=AE,
∵AF⊥DE,AD⊥AE,
∴AF=DF=EF=
DE,
∵EC⊥BC,
∴CF=
DE,
∴AF=CF,
又∵AG=GC,
∴FG⊥AC.
∴∠B=∠ACB=45°,
∵EC⊥BC,
∴∠BCE=90°,
∴∠ACE=90°-45°=45°,
∴∠B=∠ACE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS);
(2)证明:∵△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠DAE=∠CAD+∠CAE=∠CAD+∠BAD=∠BAC=90°,
∴AD⊥AE;
(3)解:FG⊥AC.
理由如下:连接CF,∵△ABD≌△ACE,

∴AD=AE,
∵AF⊥DE,AD⊥AE,
∴AF=DF=EF=
| 1 |
| 2 |
∵EC⊥BC,
∴CF=
| 1 |
| 2 |
∴AF=CF,
又∵AG=GC,
∴FG⊥AC.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,等腰三角形三线合一的性质,直角三角形斜边上的中线等于斜边的一半的性质,(3)作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x2m-1y与x5ym+n是同类项,那么(mn+5)2008=( )
| A、1 | B、-1 |
| C、1或-1 | D、无法确定 |
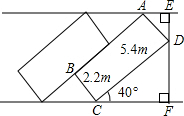 随着人民生活水平的提高,小轿车也逐渐进入千家万户.为了解决停车难问题,我县交警大队在城区划定了许多机动车停车位.如图,矩形ABCD的供一辆机动车停放的车尾示意图,已知BC=2.2m,∠DCF=40°,请计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m)
随着人民生活水平的提高,小轿车也逐渐进入千家万户.为了解决停车难问题,我县交警大队在城区划定了许多机动车停车位.如图,矩形ABCD的供一辆机动车停放的车尾示意图,已知BC=2.2m,∠DCF=40°,请计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m) 有一块三角形木板,已测得边AB=50cm,∠B=35°,∠C=75°,求该板的面积.(精确到0.1cm2)
有一块三角形木板,已测得边AB=50cm,∠B=35°,∠C=75°,求该板的面积.(精确到0.1cm2)