题目内容
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为 .
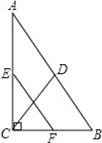

5 .
【考点】三角形中位线定理;直角三角形斜边上的中线.
【分析】已知CD是Rt△ABC斜边AB的中线,那么AB=2CD;EF是△ABC的中位线,则EF应等于AB的一半.
【解答】解:∵△ABC是直角三角形,CD是斜边的中线,
∴CD=
 AB,
AB,
又∵EF是△ABC的中位线,
∴AB=2CD=2×5=10cm,
∴EF=
 ×10=5cm.
×10=5cm.
故答案为:5.
【点评】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目

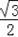
 C.
C.


 =1,则 ( )
=1,则 ( ) 2 C. x≠
2 C. x≠ D. x为任意有理数
D. x为任意有理数 