题目内容
12.在△ABC中,P为边AB上一点.(1)如图1,若∠ACP=∠B,求证:AC2=AP•AB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

分析 (1)根据相似三角形的判定定理即可得到结论;
(2)①取AP在中点G,连接MG,设AG=x,则PG=x,BG=3-x,根据三角形的中位线的性质得到MG∥AC,由平行线的性质得到∠BGM=∠A,∵∠根据相似三角形的性质得到$\frac{2x}{1}=\frac{2}{3-x}$,求得x=$\frac{3±\sqrt{5}}{2}$,即可得到结论;②过C作CH⊥AB于H,延长AB到E,使BE=BP解直角三角形得到CH=$\sqrt{3}$,HE=$\sqrt{3}$+x,根据勾股定理得到CE2=($\sqrt{3})^{2}$+9$\sqrt{3}$+x)2根据相似三角形的性质得到CE2=EP•EA列方程即可得到结论.
解答  解:(1)∵∠ACP=∠B,∠A=∠A,
解:(1)∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴$\frac{AC}{AP}=\frac{AB}{AC}$,
∴AC2=AP•AB;
(2)①取AP在中点G,连接MG,设AG=x,则PG=x,BG=3-x,
∵M是PC的中点,
∴MG∥AC,
∴∠BGM=∠A,
∵∠ACP=∠PBM,
∴△APC∽△GMB,
∴$\frac{AP}{GM}=\frac{AC}{BG}$,
即$\frac{2x}{1}=\frac{2}{3-x}$,
∴x=$\frac{3±\sqrt{5}}{2}$,
∵AB=3,
∴AP=3-$\sqrt{5}$,
∴PB=$\sqrt{5}$;
②过C作CH⊥AB于H,延长AB到E,使BE=BP,
设BP=x.
∵∠ABC=45°,∠A=60°,
∴CH=$\sqrt{3}$,HE=$\sqrt{3}$+x,
∵CE2=($\sqrt{3})^{2}$+($\sqrt{3}$+x)2,
∵PB=BE,PM=CM,
∴BM∥CE,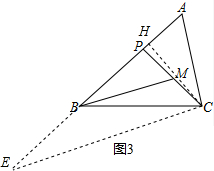
∴∠PMB=∠PCE=60°=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴$\frac{CE}{EP}=\frac{AE}{CE}$,
∴CE2=EP•EA,
∴3+3+x2+2$\sqrt{3}$x=2x(x+$\sqrt{3}$+1),
∴x=$\sqrt{7}$-1,
∴PB=$\sqrt{7}$-1.
点评 本题考查了相似三角形的判定和性质,平行线的性质,三角形的中位线的性质,勾股定理,正确作出辅助线是解题的关键.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )| A. | (40-x)(26-2x)=144×6 | B. | (40-2x)(26-x)=144×6 | C. | (40-2x)(26-x)=144÷6 | D. | (40-x)(26-2x)=144÷6 |
| A. | 乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 苹果电脑的市场占有率 | |
| C. | “我爱发明”专栏电视节目的收视率 | |
| D. | “现代”汽车每百公里的耗油量 |
| A. |  线段 | B. |  三角形 | C. |  正方形 | D. |  圆 |
| “读书节”活动计划书 | ||
| 书本类别 | A类 | B类 |
| 进价(单位:元) | 18 | 12 |
| 备注 | 1、用不超过16800元购进A、B两类图书共1000本; 2、A类图书不少于600本; … | |
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
 如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-$\frac{1}{6}$x+4,直线DG和AF交于点H.
如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-$\frac{1}{6}$x+4,直线DG和AF交于点H.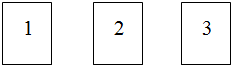 如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.
如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$. 如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.