题目内容
直径为4的圆的内接正三角形的边长为( )
分析:首先根据题意作出图形,然后由垂径定理,可得BD=
BC,求得∠BOD=
∠BOC=∠A,再利用三角函数求得BD的长,继而求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: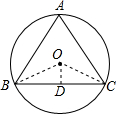 解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,
解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,
∴BD=CD=
BC,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=
∠BOC=60°,
∵直径为4,
∴OB=
×4=2,
∴BD=OB•sin∠BOD=2×
=
,
∴BC=2BD=2
,
即直径为4的圆的内接正三角形的边长为:2
.
故选C.
 解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,
解:如图:△ABC是等边三角形,过点O作OD⊥BC于D,连接OB,OC,∴BD=CD=
| 1 |
| 2 |
∵△ABC是等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=
| 1 |
| 2 |
∵直径为4,
∴OB=
| 1 |
| 2 |
∴BD=OB•sin∠BOD=2×
| ||
| 2 |
| 3 |
∴BC=2BD=2
| 3 |
即直径为4的圆的内接正三角形的边长为:2
| 3 |
故选C.
点评:此题考查了正多边形和圆的性质、垂径定理以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 圆
圆 的内接正三角形,那么∠
的内接正三角形,那么∠ ﹦ ;
﹦ ; 是圆
是圆 是圆的任意一条弦,∠
是圆的任意一条弦,∠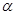 ﹒
﹒ 边形的一边,则用含
边形的一边,则用含