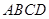题目内容
如图, 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.
(1) 的坐标;
的坐标;
(2) 时,求
时,求 的值;
的值;
(3) 为圆心,
为圆心, 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值.
 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.(1)
 的坐标;
的坐标;(2)
 时,求
时,求 的值;
的值;(3)
 为圆心,
为圆心, 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值. 
解:(1) ,
,
又∵点 在
在 轴的正半轴上,
轴的正半轴上,
∴点 的坐标为(0,3)
的坐标为(0,3)
(2)当点 在点
在点 右侧时,
右侧时,
如图2.若 ,得
,得 .
.
故 ,此时
,此时 .
.
当点 在点
在点 左侧时,
左侧时,
如图3,由 ,得
,得 ,
,
故 .此时
.此时 .
. 的值为
的值为 或
或

(3)由题意知,若 与四边形
与四边形 的边相切,
的边相切,
有以下三种情况:
①当 与
与 相切于点
相切于点 时,有
时,有 ,从而
,从而 得到
得到 .此时
.此时 .
.
②当 与
与 相切于点
相切于点 时,有
时,有 ,即点
,即点 与点
与点 重合,此时
重合,此时 .
.
③当 与
与 相切时,由题意,
相切时,由题意, ,
, 点
点 为切点,
为切点,
如图4. .于是
.于是 .
.
解处 .
. 的值为1或4或5.6.
的值为1或4或5.6.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目

 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒. 时,求
时,求 为半径的
为半径的 随点
随点

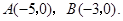 点
点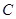 在
在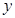 轴的正半轴上,
轴的正半轴上,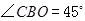 ,
,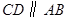 ,
,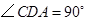 .点
.点 从点
从点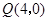 出发,沿
出发,沿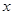 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.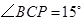 时,求
时,求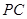 为半径的
为半径的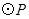 随点
随点