题目内容
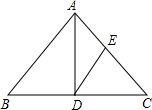
如图所示,已知AD是等腰△ABC底边上的高,且tan∠B= ,AC上有一点E,满足AE:CE=2:3,则tan∠ADE的值是( )
,AC上有一点E,满足AE:CE=2:3,则tan∠ADE的值是( )
A.

B.

C.

D.

【答案】分析:过E点作CD的平行线交AD于F,设AE=2a,则CE=3a.tan∠C= ,EF和DF分别可用a的代数式来表达,即可得出tan∠ADE的值.
,EF和DF分别可用a的代数式来表达,即可得出tan∠ADE的值.
解答: 解:过E点作CD的平行线交AD于F.如图:
解:过E点作CD的平行线交AD于F.如图:
∵AD是等腰△ABC底边上的高,tan∠B= ,
,
∴EF⊥AD,tan∠C= .
.
设AE=2a,
∵AE:CE=2:3,
∴CE=3a,AC=5a.
∵tan∠C= ,
,
∴sin∠C= ,cos∠C=
,cos∠C= .
.
在直角△ADC中,
AD=ACsin∠C=5a× =3a.
=3a.
在直角△AFE中,
AF=AE×sin∠AEF=AE×sin∠C=2a× =
= .
.
EF=AE×cos∠AEF=AE×cos∠C=2a× =
= .
.
在直角△DFE中,
tan∠ADE= .
.
故选B.
点评:考查等腰三角形的性质和三角函数的性质.
 ,EF和DF分别可用a的代数式来表达,即可得出tan∠ADE的值.
,EF和DF分别可用a的代数式来表达,即可得出tan∠ADE的值.解答:
 解:过E点作CD的平行线交AD于F.如图:
解:过E点作CD的平行线交AD于F.如图:∵AD是等腰△ABC底边上的高,tan∠B=
 ,
,∴EF⊥AD,tan∠C=
 .
.设AE=2a,
∵AE:CE=2:3,
∴CE=3a,AC=5a.
∵tan∠C=
 ,
,∴sin∠C=
 ,cos∠C=
,cos∠C= .
.在直角△ADC中,
AD=ACsin∠C=5a×
 =3a.
=3a.在直角△AFE中,
AF=AE×sin∠AEF=AE×sin∠C=2a×
 =
= .
.EF=AE×cos∠AEF=AE×cos∠C=2a×
 =
= .
.在直角△DFE中,
tan∠ADE=
 .
.故选B.
点评:考查等腰三角形的性质和三角函数的性质.

练习册系列答案
相关题目
 如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=
如图所示,已知AD是等腰△ABC底边上的高,且tan∠B=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 23、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF.
23、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF. 17、如图所示,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,
17、如图所示,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,
 如图所示,已知AD是△ABC的中线,在AD及延长线上截取DE=DF,连接CE,BF.
如图所示,已知AD是△ABC的中线,在AD及延长线上截取DE=DF,连接CE,BF.