题目内容
对于一元二次方程x2-3x=4，下列说法正确的是（ ）
| A、有两个不相等的实根 |
| B、有两个相等的实根 |
| C、没有实根 |
| D、只有一个实数根 |
考点：根的判别式
专题：
分析：判断上述方程的根的情况，只要看根的判别式值的符号就可以了．
解答：解：原方程化为一般形式为x2-3x-4=0，
∵a=1，b=-3，c=-4，
∴△=b2-4ac=（-3）2-4×1×（-4）=25＞0，
∴方程有两个不相等实数根．
故选：A．
∵a=1，b=-3，c=-4，
∴△=b2-4ac=（-3）2-4×1×（-4）=25＞0，
∴方程有两个不相等实数根．
故选：A．
点评：此题考查一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
如图，点A、B、C、D在一次函数y=-2x+m的图象上，它们的横坐标分别是-1、0、3、7，分别过这些点作x轴、y轴的垂线，得到三个矩形，那么这三个矩形的周长和为（ ）| A、6m-14 | B、52 |
| C、48 | D、8m-72 |
|-0.5|的倒数是（ ）
| A、0.5 | ||
| B、-2 | ||
| C、2 | ||
D、
|
内切两圆的半径分别为2cm和4cm，则两圆的圆心距是（ ）
| A、1cm | B、2cm |
| C、3cm | D、5cm |
抛物线y=ax2+bx+c如图，对称轴是x=-1，则下列结论中正确的是（ ）| A、b＞0 |
| B、4a+c＜2b |
| C、a-b＜0 |
| D、c-a＞1 |
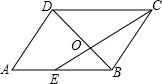如图，在平行四边形ABCD中，E是AB的中点，CE和BD交于点O，若CE=6，则CO的长为（ ）| A、5 | ||
| B、4 | ||
| C、3 | ||
D、
|