题目内容
 如图,△ABC的内切圆⊙O与各边相切于D,E,F,则点O是△ABC的
如图,△ABC的内切圆⊙O与各边相切于D,E,F,则点O是△ABC的
- A.三条中线交点
- B.三条高线交点
- C.三条角平分线交点
- D.三边中垂线交点
C
分析:因为O为圆心,所以OE=OF=OD,故点O是△DEF的三边中垂线交点,还是△ABC的三条角平分线的交点.
解答:∵△ABC的内切圆与各边相切于D,E,F,OE=OF=OD,
则可知点O是DE、DF、EF中垂线上的点,
∴点O是△DEF的三边中垂线交点,则又是△ABC的三条角平分线的交点.
故选C.
点评:此题考查了三角形内切圆的圆心是三个内角平分线的交点,外接圆的圆心是三边中垂线交点.
分析:因为O为圆心,所以OE=OF=OD,故点O是△DEF的三边中垂线交点,还是△ABC的三条角平分线的交点.
解答:∵△ABC的内切圆与各边相切于D,E,F,OE=OF=OD,
则可知点O是DE、DF、EF中垂线上的点,
∴点O是△DEF的三边中垂线交点,则又是△ABC的三条角平分线的交点.
故选C.
点评:此题考查了三角形内切圆的圆心是三个内角平分线的交点,外接圆的圆心是三边中垂线交点.

练习册系列答案
相关题目
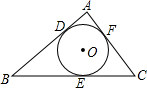 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.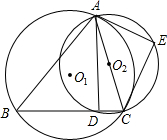 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3
