Question

【题目】已知函数，其自变量的取值范围是．当时，；当时，．

（1）根据给定的条件，求出的函数解析式；

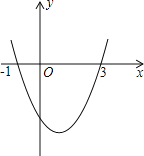
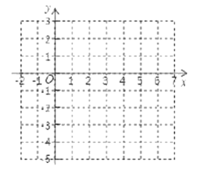
（2）根据你所求的函数解析式，选取适当的自变量完成如表，并在下面的平面直角坐标系中描点并画出函数的大致图象：

（3）请画出的图象，并结合图象直接写出：当时，的取值范围是 ．

Answer 1

【答案】（1）；（2）-1，-5，-2，，，，，-5，见解析；（3）见解析，-1<x<2

【解析】

（1）利用待定系数法求解即可．

（2）在x>-2的条件下，取x的一些值，计算出对应的y值，即可完成表格；再根据表格数据描点、连线即可画出函数的大致图象．

（3）先画函数的图象，然后找出y1在y2图象上方的部分对应的x的取值即可．

,

把,；,代入,

得

解得,

的函数解析式为；

填表如下：

x			0	1	2	3	4	5	6
y

图象如图所示：

函数的图象如图所示，由图可知,当时,x的取值范围是．