题目内容
5．若等腰三角形的腰长为10，底边长为16，则此三角形的面积是（ ）| A． | 160 | B． | 80 | C． | 96 | D． | 48 |
分析 等腰三角形ABC，AB=AC，要求三角形的面积，可以先作出BC边上的高AD，则在Rt△ADB中，利用勾股定理就可以求出高AD，就可以求出三角形的面积．
解答 
解：作AD⊥BC于D，
∵AB=AC，
∴BD=BC=8cm，
∴AD=$\sqrt{{AC}^{2}-{CD}^{2}}$=6，
∴S△ABC=$\frac{1}{2}$BC•AD=48．
故选D．
点评 本题主要考查了勾股定理及等腰三角形的性质，利用勾股定理求出三角形的高AD是解答本题的关键．
练习册系列答案
相关题目
16．下列说法错误的是（ ）
| A． | 1的平方根是±1 | B． | -1的立方根是-1 | ||
| C． | $\sqrt{2}$是2的一个平方根 | D． | -3是$\sqrt{（-3）^{2}}$的一个平方根 |
13．
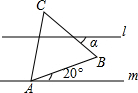如图，l∥m，等边△ABC的顶点A在m上，则∠α的度数为（ ）
如图，l∥m，等边△ABC的顶点A在m上，则∠α的度数为（ ）| A． | 20° | B． | 40° | C． | 50° | D． | 60° |
17．a＜b，则下列不等式一定成立的是（ ）
| A． | a2＜b2 | B． | ac2＜bc2 | C． | ac＜bc | D． | a-b＜0 |
14．
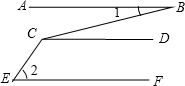如图，若AB∥CD，CD∥EF，那么∠BCE=（ ）
如图，若AB∥CD，CD∥EF，那么∠BCE=（ ）| A． | ∠1+∠2 | B． | 180°-∠1+∠2 | C． | ∠2-∠1 | D． | 180°-∠2+∠1 |
15．若y轴上的点A到x轴的距离为3，则点A的坐标为（ ）
| A． | （3，0） | B． | （3，0）或（-3，0） | C． | （0，3） | D． | （0，3）或（0，-3） |