题目内容
△ABC内接于⊙O,且AB=AC,⊙O的半径等于6cm,O点到BC的距离OE等于3cm,则AC的长为________.
6 cm或6cm
cm或6cm
分析:此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AC的长.
解答:分两种情况:
(1)假若∠A是锐角,△ABC是锐角三角形,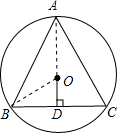
∵AB=AC
∴点A是优弧 的中点
的中点
∵OD⊥BC且AB=AC
根据垂径定理推论可知,DO的延长线必过点A,连接BO
∵BO=6,OD=3,
∴BD= =
= =3
=3
在Rt△ADB中,AD=DO+AO=6+3=9,
∴AB=AC= =6
=6 cm;
cm;
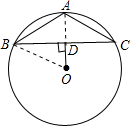 (2)若∠A是钝角,则△ABC是钝角三角形,
(2)若∠A是钝角,则△ABC是钝角三角形,
如图添加辅助线及求出BD=3
在Rt△ADB中,AD=AO-DO=6-3=3,
∴AB=AC=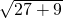 =6cm.
=6cm.
综上所述AB=6 cm或6cm.
cm或6cm.
点评:此题主要是勾股定理和垂径定理的运用.注意:三角形的外心可能在三角形的外部,可能在三角形的内部,也可能在三角形的一边上,即直角三角形的外心在其斜边的中点.
 cm或6cm
cm或6cm分析:此题分情况考虑:当三角形的外心在三角形的内部时,根据勾股定理求得BD的长,再根据勾股定理求得AB的长;当三角形的外心在三角形的外部时,根据勾股定理求得BD的长,再根据勾股定理求得AC的长.
解答:分两种情况:
(1)假若∠A是锐角,△ABC是锐角三角形,

∵AB=AC
∴点A是优弧
 的中点
的中点∵OD⊥BC且AB=AC
根据垂径定理推论可知,DO的延长线必过点A,连接BO
∵BO=6,OD=3,
∴BD=
 =
= =3
=3
在Rt△ADB中,AD=DO+AO=6+3=9,
∴AB=AC=
 =6
=6 cm;
cm; (2)若∠A是钝角,则△ABC是钝角三角形,
(2)若∠A是钝角,则△ABC是钝角三角形,如图添加辅助线及求出BD=3

在Rt△ADB中,AD=AO-DO=6-3=3,
∴AB=AC=
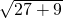 =6cm.
=6cm.综上所述AB=6
 cm或6cm.
cm或6cm.点评:此题主要是勾股定理和垂径定理的运用.注意:三角形的外心可能在三角形的外部,可能在三角形的内部,也可能在三角形的一边上,即直角三角形的外心在其斜边的中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
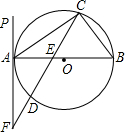 如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B,
如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B, (2013•和平区一模)如图,△ABC内接于⊙O,AD是∠ABC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )
(2013•和平区一模)如图,△ABC内接于⊙O,AD是∠ABC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( ) 如图,已知△ABC内接于⊙O,∠BAC=60°,AD⊥BC于D,BE⊥AC交AD于H,若CF是⊙O的直径.
如图,已知△ABC内接于⊙O,∠BAC=60°,AD⊥BC于D,BE⊥AC交AD于H,若CF是⊙O的直径. 如图,△ABC内接于⊙O,点P在弧AC上移动(点P不与点A、C重合),若∠B=40°,则α的变化范围是
如图,△ABC内接于⊙O,点P在弧AC上移动(点P不与点A、C重合),若∠B=40°,则α的变化范围是