题目内容
已经反比例函数y=
(k不等于0)和一次函数y=x+n相交于A、B两点,他们的横坐标分别是-1和4,则不等式-
>-x+n的解集是 .
| k |
| x |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据反比例函数y=
(k不等于0)和一次函数y=x+n相交于A、B两点,可得反比例函数y=-
(k不等于0)和一次函数y=-x+n相交于A1、B1两点,可得A、B与A1、B1关于y轴对称,根据图象与不等式的关系,可得答案.
| k |
| x |
| k |
| x |
解答:解;∵反比例函数y=
(k不等于0)和一次函数y=x+n相交于A、B两点,他们的横坐标分别是-1和4,
反比例函数y=-
(k不等于0)和一次函数y=-x+n相交于A1、B1两点,(1,y1)(-4,y2),
不等式-
>-x+n的解集是-4<x<0后x>1,
故答案为:-4<x<0或x>1.
| k |
| x |
反比例函数y=-
| k |
| x |
不等式-
| k |
| x |
故答案为:-4<x<0或x>1.
点评:本题考查了反比例函数与一次函数的交点问题,系数互为相反数的函数图象关于y轴对称是解题关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
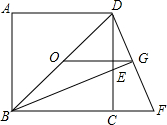 如图,正方形ABCD的中心为O,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
如图,正方形ABCD的中心为O,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG. 在一次数学活动课上,小李同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上点F处,如图,若CD=16cm,BE=10cm,则AD=
在一次数学活动课上,小李同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上点F处,如图,若CD=16cm,BE=10cm,则AD= 如图,如果∠1=∠3,能判定
如图,如果∠1=∠3,能判定 由若干个大小相同的小正方体组成的几何体的三视图如图,则这个几何体只能是( )
由若干个大小相同的小正方体组成的几何体的三视图如图,则这个几何体只能是( )


