题目内容
为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,若测得∠ACB=30°,量得BC=60m,那么河宽AB为
- A.20
 m
m - B.40
 m
m - C.30
 m
m - D.60
 m
m
A
分析:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60.根据三角函数定义求解.
解答: 解:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60,
解:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60,
∴tan∠ACB= ,
,
即AB=BCtan∠ACB
=60tan30°
=60×
=20 .
.
故选A.
点评:解此题的关键是把实际问题转化为数学问题,只要画出图形,就能把它抽象到直角三角形中,利用正切来解决问题.
分析:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60.根据三角函数定义求解.
解答:
 解:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60,
解:如图,△ABC中,CB⊥AB,∠ACB=30°,BC=60,∴tan∠ACB=
 ,
,即AB=BCtan∠ACB
=60tan30°
=60×

=20
 .
.故选A.
点评:解此题的关键是把实际问题转化为数学问题,只要画出图形,就能把它抽象到直角三角形中,利用正切来解决问题.

练习册系列答案
相关题目
为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,若测得∠ACB=30°,量得BC=60m,那么河宽AB为( )
A、20
| ||
B、40
| ||
C、30
| ||
D、60
|
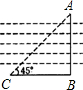 (2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
(2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )

 米
米 米
米